Točno
28. studenoga 2022. 22:43 (3 godine, 2 mjeseci)
Dani su pozitivni realni brojevi

,
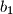
,
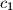
,

,
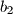
,
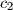
za koje vrijedi
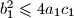
i
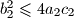
.
Dokaži da vrijedi
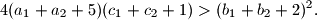
%V0
Dani su pozitivni realni brojevi $a_1$, $b_1$, $c_1$, $a_2$, $b_2$, $c_2$ za koje vrijedi $b_1^2 \leqslant 4a_1c_1$ i $b_2^2\leqslant 4a_2c_2$.
Dokaži da vrijedi $$4(a_1+a_2+5)(c_1+c_2+1)>(b_1+b_2+2)^2.$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Ovo mi se čini vrlo lagano preko CSB nejednakosti
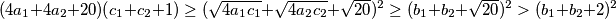
Valjda ovo valja
Ovo mi se čini vrlo lagano preko CSB nejednakosti
$$(4a_1 + 4a_2 + 20)(c_1 + c_2 + 1) \geq (\sqrt{4a_1c_1} + \sqrt{4a_2c_2} + \sqrt{20})^2 \geq (b_1 + b_2 + \sqrt{20})^2 > (b_1 + b_2 + 2)^2$$
Valjda ovo valja
| 29. studenoga 2022. 14:07 | 11235 | Točno |