Točno
28. studenoga 2022. 23:22 (3 godine, 2 mjeseci)
U svaki vrh pravilnog  -erokuta je upisan ili broj
-erokuta je upisan ili broj  ili broj
ili broj  . Ni za koja tri uzastopna vrha upisani brojevi nisu jednaki, a ukupno je dvadeset puta upisan broj
. Ni za koja tri uzastopna vrha upisani brojevi nisu jednaki, a ukupno je dvadeset puta upisan broj  i trideset puta upisan broj
i trideset puta upisan broj  . Za svaki vrh izračunamo umnožak broja u tom vrhu s brojevima u dvama susjednim vrhovima, a zatim zbrojimo sve takve umnoške.
. Za svaki vrh izračunamo umnožak broja u tom vrhu s brojevima u dvama susjednim vrhovima, a zatim zbrojimo sve takve umnoške.
Dokaži da rezultat ne ovisi o rasporedu brojeva i
i  te odredi taj rezultat.
te odredi taj rezultat.
 -erokuta je upisan ili broj
-erokuta je upisan ili broj  ili broj
ili broj  . Ni za koja tri uzastopna vrha upisani brojevi nisu jednaki, a ukupno je dvadeset puta upisan broj
. Ni za koja tri uzastopna vrha upisani brojevi nisu jednaki, a ukupno je dvadeset puta upisan broj  i trideset puta upisan broj
i trideset puta upisan broj  . Za svaki vrh izračunamo umnožak broja u tom vrhu s brojevima u dvama susjednim vrhovima, a zatim zbrojimo sve takve umnoške.
. Za svaki vrh izračunamo umnožak broja u tom vrhu s brojevima u dvama susjednim vrhovima, a zatim zbrojimo sve takve umnoške.Dokaži da rezultat ne ovisi o rasporedu brojeva
 i
i  te odredi taj rezultat.
te odredi taj rezultat. Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Moguće su 2 kombinacije za okolicu svakog vrha (1 , 2 , 2) i svaka permutacija i (2 , 1, 1) i svaka permutacija.
Oznaćimo broj vrhova prve sa  a drugu sa
a drugu sa  Znamo da je
Znamo da je 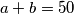 Ali također se možemo koristit i činjenicom da ima
Ali također se možemo koristit i činjenicom da ima  dvica i
dvica i  jedinica. To ćemo koristit za zbroj.
jedinica. To ćemo koristit za zbroj.
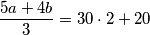
Znaći ovo nam uglavnom govori da sa zvaki vrh kojem je okolica (2 , 2 ,1) da je zbroj tih 3 jednak  . Također i za (1 , 1 ,2) je zbroj
. Također i za (1 , 1 ,2) je zbroj  . Djelimo sa 3 jer smo 3 puta brojali isti broj tako da je
. Djelimo sa 3 jer smo 3 puta brojali isti broj tako da je 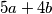 trostruka suma svih vrhova. Sad vidimo kako god možemo poredati ovo imat ćemo isti broj vrhova kojima će umnožak biti
trostruka suma svih vrhova. Sad vidimo kako god možemo poredati ovo imat ćemo isti broj vrhova kojima će umnožak biti  i isti broj vrhova kojima će umnožak biti
i isti broj vrhova kojima će umnožak biti 
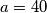
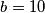 Prema tome će ta čudma suma umnoška biti
Prema tome će ta čudma suma umnoška biti
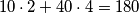
 Školjka
Školjka