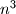 jediničnih kockica sastavio veliku kocku brida duljine
jediničnih kockica sastavio veliku kocku brida duljine  i zatim je neke od šest strana velike kocke obojao, a neke nije. Kada je rastavio veliku kocku, otkrio je da točno
i zatim je neke od šest strana velike kocke obojao, a neke nije. Kada je rastavio veliku kocku, otkrio je da točno 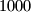 jediničnih kockica nema niti jednu obojanu stranu. Pokaži da je to zaista moguće i odredi broj strana velike kocke koje je Ivica obojao.
jediničnih kockica nema niti jednu obojanu stranu. Pokaži da je to zaista moguće i odredi broj strana velike kocke koje je Ivica obojao. Kliknite ovdje kako biste prikazali rješenje.
Logično imamo 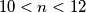 Ili ti
Ili ti 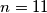 Sad imamo da je unutarnji volumen
Sad imamo da je unutarnji volumen 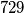 Tako da bi vanjski trebao biti
Tako da bi vanjski trebao biti 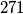 Sada rješavamo
Sada rješavamo
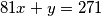
x je koliko ima neobojanih strana a y je ostatak ili ti međuprostor dvije neobojane strane za koju nemam baš nešto generalno ali bit će malen
za  ostatka nema tako da to nemože za
ostatka nema tako da to nemože za 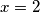 maksimalan ostatak je
maksimalan ostatak je  tako da to također nemože
tako da to također nemože 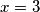 je stvarno i zadnji broj koji možemo uzet u obzir.
je stvarno i zadnji broj koji možemo uzet u obzir.
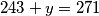
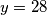 Taj ostatak je moguć kad su 3 neobojane stranice djele 1 neobojan vrh. Jer je
Taj ostatak je moguć kad su 3 neobojane stranice djele 1 neobojan vrh. Jer je 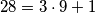
Tako da to je jedna i jedina mogučnost. Tvrdnja je moguça i broj obojanih strana je  ili ti
ili ti 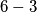
Ocjene: (1)
Komentari:
U rješenju se previše koncentriraš na krive stvari.
Npr. zadatak kaže pokaži da je moguće i odredi broj strana. Ti si broj strana odredio riječima "a pa logično je da imamo...", dakle tu bi izgubio dosta bodova bez dobrog rješenja. Tu bi trebalo dodati rečenicu npr. Kako je 1000 = 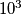 , onda iz činjenice da je
, onda iz činjenice da je 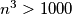 (jer su neke kockice obojane) mogu zaključiti
(jer su neke kockice obojane) mogu zaključiti 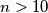 . Slično, ako obojim sve vanjske strane velike kocke, dobio bih
. Slično, ako obojim sve vanjske strane velike kocke, dobio bih 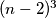 manjih kocaka u njenoj unutrašnjosti koje nisu obojane, ali kako su neke strane ipak ostale neobojane, onda sigurno vrijedi
manjih kocaka u njenoj unutrašnjosti koje nisu obojane, ali kako su neke strane ipak ostale neobojane, onda sigurno vrijedi 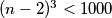 iz čega slijedi
iz čega slijedi 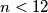 . (Dakle treba opravdati brojeve i znakove stroge nejednakosti. Nakon toga se slažem da je jedino rješenje
. (Dakle treba opravdati brojeve i znakove stroge nejednakosti. Nakon toga se slažem da je jedino rješenje 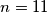 trivijalno.)
trivijalno.)
Nadalje, ti zadatku pristupaš kao da želiš po slučajevima odrediti sva takva bojanja. To nije potrebno jer se pokazuje da je nešto moguće primjerom. Dakle jedini dio dokaza nakon prve rečenice (koju treba doraditi s barem dvije) koji ti treba je "Taj ostatak je moguć kad su 3 neobojane stranice dijele 1 neobojan vrh." (eventualno provjera, ali nju bi se složio da je očito iz konstrukcije da radi).
 Školjka
Školjka