Točno
3. prosinca 2022. 19:33 (3 godine, 3 mjeseci)
Neka se točke

i

nalaze redom na stranicama

i

trokuta

. Simetrale kutova
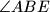
i
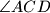
sijeku se u točki

. Dokažite da je
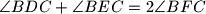
.
%V0
Neka se točke $D$ i $E$ nalaze redom na stranicama $AB$ i $AC$ trokuta $ABC$. Simetrale kutova $\angle ABE$ i $\angle ACD$ sijeku se u točki $F$. Dokažite da je $\angle BDC + \angle BEC = 2 \angle BFC$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
\url{https://ibb.co/87h2cNG}
Označio sam kutove kao na slici sa $\alpha$ , $\alpha '$ , $\beta$ , $\beta '$ , $\gamma$
Iz slike možemo uočit dvije jednakosti
$$\gamma + \alpha ' - \beta - \beta ' = 0$$
$$\gamma + \beta ' - \alpha - \alpha ' = 0$$
Zbrajanjem dobijamo
$$2\gamma = \alpha + \beta$$
Odakle te jednakosti?
Evo prva dolazi iz trokuta $\Delta BFG$ gdje je $G$ sječište stranica $CF$ i $BE$
Iz tog trokuta imamo
$$\gamma + 180 - (\beta + \beta ' ) + \alpha ' = 180$$
Analogno dobijemo i za drugi trokut sa vrhom u $C$ i kutem $\beta '$
| 6. prosinca 2022. 21:09 | iivan | Točno |
 ,
, 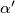 ,
,  ,
, 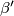 ,
, 
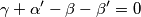
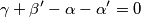 Zbrajanjem dobijamo
Zbrajanjem dobijamo 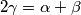
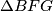 gdje je
gdje je  sječište stranica
sječište stranica 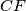 i
i  Iz tog trokuta imamo
Iz tog trokuta imamo 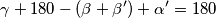
 i kutem
i kutem 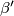
 Školjka
Školjka  i
i  nalaze redom na stranicama
nalaze redom na stranicama  i
i  trokuta
trokuta  . Simetrale kutova
. Simetrale kutova 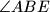 i
i 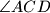 sijeku se u točki
sijeku se u točki  . Dokažite da je
. Dokažite da je 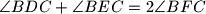 .
.