Točno
15. prosinca 2022. 21:32 (3 godine, 2 mjeseci)
Dijagonale tetivnog četverokuta

sijeku se u točki

. Kružnica

opisana trokutu
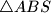
siječe pravac

u točki

, a kružnica

opisana trokutu
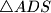
siječe pravac

u točki

. Dokažite da su točke

,

i

kolinearne.
%V0
Dijagonale tetivnog četverokuta $ABCD$ sijeku se u točki $S$. Kružnica $k_1$ opisana trokutu $\triangle ABS$ siječe pravac $BC$ u točki $M$, a kružnica $k_2$ opisana trokutu $\triangle ADS$ siječe pravac $CD$ u točki $N$. Dokažite da su točke $S$, $M$ i $N$ kolinearne.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
https://ibb.co/r0dFxQg Ignorirajte bojice koristia sam ih samo da pratim koji su mi tetivni četverokuti.
Ugl samo sa stavia da mi je 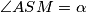
Onda ako dokažem da je 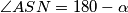 , što i jesam , točke su kolinearne.
, što i jesam , točke su kolinearne.
Ugl samo tetivni četverokuti
\url{https://ibb.co/r0dFxQg}
Ignorirajte bojice koristia sam ih samo da pratim koji su mi tetivni četverokuti.
Ugl samo sa stavia da mi je $\angle ASM = \alpha$
Onda ako dokažem da je $\angle ASN = 180 - \alpha$ , što i jesam , točke su kolinearne.
Ugl samo tetivni četverokuti
| 18. prosinca 2022. 14:48 | iivan | Točno |
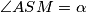
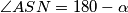 , što i jesam , točke su kolinearne.
, što i jesam , točke su kolinearne. Školjka
Školjka  sijeku se u točki
sijeku se u točki  . Kružnica
. Kružnica  opisana trokutu
opisana trokutu  siječe pravac
siječe pravac  u točki
u točki  , a kružnica
, a kružnica  opisana trokutu
opisana trokutu  siječe pravac
siječe pravac  u točki
u točki  . Dokažite da su točke
. Dokažite da su točke