Točno
3. prosinca 2022. 23:59 (3 godine, 3 mjeseci)
Zadan je tetivni četverokut

čije su dijagonale

i

međusobno okomite. Neka je

sjecište dijagonala, a

nožište visine iz vrha

na stranicu

. Dokažite da vrijedi
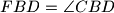
.
%V0
Zadan je tetivni četverokut $ABCD$ čije su dijagonale $AC$ i $BD$ međusobno okomite. Neka je $E$ sjecište dijagonala, a $F$ nožište visine iz vrha $B$ na stranicu $AD$. Dokažite da vrijedi $FBD = \angle CBD$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
https://ibb.co/r706sV8 Mislim da slika sve govori ali ugl. Prema tetivnim četverokutima 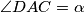 I onda samo pravi kutovi.
I onda samo pravi kutovi.
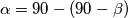
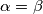
\url{https://ibb.co/r706sV8}
Mislim da slika sve govori ali ugl.
Prema tetivnim četverokutima $\angle DAC = \alpha$
I onda samo pravi kutovi.
$$\alpha = 90 - (90 - \beta )$$
$$\alpha = \beta$$
| 7. prosinca 2022. 16:53 | iivan | Točno |
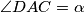 I onda samo pravi kutovi.
I onda samo pravi kutovi.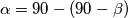
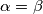
 Školjka
Školjka  čije su dijagonale
čije su dijagonale  i
i  međusobno okomite. Neka je
međusobno okomite. Neka je  sjecište dijagonala, a
sjecište dijagonala, a  nožište visine iz vrha
nožište visine iz vrha  na stranicu
na stranicu  . Dokažite da vrijedi
. Dokažite da vrijedi 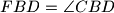 .
.