Točno
4. prosinca 2022. 15:24 (3 godine, 3 mjeseci)
Na stranici

trokuta

leže točke

,

,

tako da je

između

i

, a

između

i

. Ako je
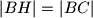
,
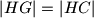
,
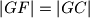
,
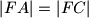
te
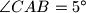
. Izračunajte koliki je

.
%V0
Na stranici $AB$ trokuta $\triangle ABC$ leže točke $F$, $G$, $H$ tako da je $F$ između $A$ i $G$, a $H$ između $G$ i $B$. Ako je $|BH| = |BC|$, $|HG| = |HC|$, $|GF| = |GC|$, $|FA| = |FC|$ te $\angle CAB = 5^{\circ}$. Izračunajte koliki je $\angle ABC$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
https://ibb.co/Wc1MF6T Mislim da je na slici sve objašnjeno. Nemojte da vas crtice zbune jer sam ih malo glupo stavio.
Ugl šta ideš desno to se duplaju kutovi. Radi toga što je vanjski kut zbroj nasuprotna dva unutarnja. I zadnji kut je samo  I da slika nije nacrtana kako bi trebala biti.
I da slika nije nacrtana kako bi trebala biti.
\url{https://ibb.co/Wc1MF6T}
Mislim da je na slici sve objašnjeno. Nemojte da vas crtice zbune jer sam ih malo glupo stavio.
Ugl šta ideš desno to se duplaju kutovi. Radi toga što je vanjski kut zbroj nasuprotna dva unutarnja.
I zadnji kut je samo $180 - 2\cdot 40 = 100$
I da slika nije nacrtana kako bi trebala biti.
| 7. prosinca 2022. 17:06 | iivan | Točno |
 I da slika nije nacrtana kako bi trebala biti.
I da slika nije nacrtana kako bi trebala biti.  Školjka
Školjka  trokuta
trokuta  leže točke
leže točke  ,
,  ,
,  tako da je
tako da je  i
i  . Ako je
. Ako je 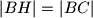 ,
, 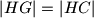 ,
, 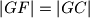 ,
, 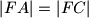 te
te 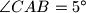 . Izračunajte koliki je
. Izračunajte koliki je  .
.