Točno
14. prosinca 2022. 14:56 (3 godine, 2 mjeseci)
Točke

i

su redom središta opisane i upisane kružnice trokuta. Izrazite
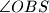
pomoću kuteva

,

i

.
%V0
Točke $O$ i $S$ su redom središta opisane i upisane kružnice trokuta. Izrazite $\angle OBS$ pomoću kuteva $\alpha$, $\beta$ i $\gamma$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Neka je |∠OBS|=b/2-δ
Kako je O srediste opisane kruznice, |OA|=|OB|=|OC|
△ABO, △BCO i △CAO su jednakokracni pa vrijedi |∠OBA| = |∠OAB| = δ
|∠OBC| = |∠BCO| = β-δ i |∠OAC| = |∠ACO| = α-δ
γ = |∠BCO|+|∠ACO| = (β-δ)+(α-δ)
β-δ+α-δ-γ = 0 pa je 2δ = β+α-γ tj. δ = (β+α-γ)/2
|∠OBS| = b/2-δ = b/2-(β+α-γ)/2 = (β-β-α+γ)/2 = (γ-α)/2
Neka je |∠OBS|=b/2-δ \\
Kako je O srediste opisane kruznice, |OA|=|OB|=|OC| \\
△ABO, △BCO i △CAO su jednakokracni pa vrijedi |∠OBA| = |∠OAB| = δ \\
|∠OBC| = |∠BCO| = β-δ i |∠OAC| = |∠ACO| = α-δ \\
γ = |∠BCO|+|∠ACO| = (β-δ)+(α-δ) \\
β-δ+α-δ-γ = 0 pa je 2δ = β+α-γ tj. δ = (β+α-γ)/2 \\
|∠OBS| = b/2-δ = b/2-(β+α-γ)/2 = (β-β-α+γ)/2 = (γ-α)/2
| 18. prosinca 2022. 14:40 | iivan | Točno |
 Školjka
Školjka  i
i  su redom središta opisane i upisane kružnice trokuta. Izrazite
su redom središta opisane i upisane kružnice trokuta. Izrazite 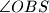 pomoću kuteva
pomoću kuteva  ,
,  i
i  .
.