Točno
8. prosinca 2022. 01:04 (3 godine, 2 mjeseci)
Pokažite da za svaka dva pozitivna broja

i

vrijedi nejednakost
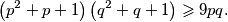
%V0
Pokažite da za svaka dva pozitivna broja $p$ i $q$ vrijedi nejednakost $$\left(p^2+p+1\right)\left(q^2+q+1\right) \geqslant 9pq \text{.}$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Distribucija
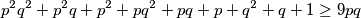
Oduzmimo 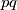
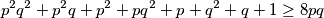
AG- nejednakosti ![p^2q + pq^2 + 1 \geq 3\sqrt[3]{p^2qpq^21}](/media/m/1/e/a/1eaaefe21f7ed7f0b8417793bdf6749a.png)
![p^2q^2 + p^2 + q^2 + p + q \geq 5\sqrt[5]{p^2q^2p^2q^2pq}](/media/m/1/2/6/126da02a5d8467efa0b1fe647bddf84f.png)
Zbroji i toe to
Distribucija
$$p^2q^2 + p^2q + p^2 + pq^2 + pq + p + q^2 + q + 1 \geq 9pq$$
Oduzmimo $pq$
$$p^2q^2 + p^2q + p^2 + pq^2 + p + q^2 + q + 1 \geq 8pq$$
AG- nejednakosti
$$p^2q + pq^2 + 1 \geq 3\sqrt[3]{p^2qpq^21}$$
$$p^2q^2 + p^2 + q^2 + p + q \geq 5\sqrt[5]{p^2q^2p^2q^2pq}$$
Zbroji i toe to