Neocijenjeno
8. prosinca 2022. 00:41 (2 godine, 2 mjeseci)
Ako su
,
,
pozitivni realni brojevi takvi da je
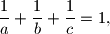
dokažite nejednakost
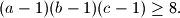
%V0
Ako su $a$, $b$, $c$ pozitivni realni brojevi takvi da je $$
\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=1,
$$ dokažite nejednakost $$
(a-1)(b-1)(c-1)\geq 8.
$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Čim sam vidio ovo pomislio sam na CSB
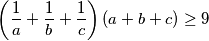
Al onda sam skužia da mi to nepomaže.
Ali zapravo pomaže. Jer tamo imamo
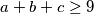
A to je isto kao i
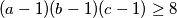
Iz početne imamo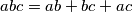 
Tako da dodamo li to našoj "točnoj" nejednakosti. Imamo
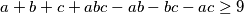Sad oduzmemo 1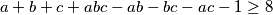 
I to se faktorizira u originalnu nejednakost.
Čim sam vidio ovo pomislio sam na CSB
$$\left(\frac{1}{a} + \frac{1}{b} + \frac{1}{c}\right)(a + b + c) \geq 9$$
Al onda sam skužia da mi to nepomaže.
Ali zapravo pomaže. Jer tamo imamo
$$a + b + c \geq 9$$
A to je isto kao i
$$(a - 1)(b - 1)(c - 1) \geq 8$$
Iz početne imamo $abc = ab + bc + ac$
Tako da dodamo li to našoj "točnoj" nejednakosti. Imamo
$$a + b + c + abc - ab - bc - ac \geq 9$$
Sad oduzmemo 1
$$a + b + c + abc - ab - bc - ac - 1 \geq 8$$
I to se faktorizira u originalnu nejednakost.
Školjka