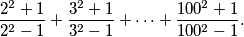Točno
7. prosinca 2022. 01:20 (3 godine, 2 mjeseci)
Izračunaj zbroj 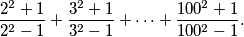
Izračunaj zbroj
$$ \frac{2^2 + 1}{2^2 - 1} + \frac{3^2 + 1}{3^2 - 1} + \dots + \frac{100^2 + 1}{100^2 - 1} \text{.} $$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kao prvo najbolje mi izgleda da izvućem jedinicu iz svakog razlomka na način : 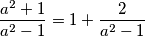
Sad sve to mogu zapisat kao
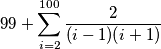
Sad ovo je samo "teleskopiranje"
Tako da idemo rastavit na parcijalne razlomke.
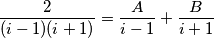
Obično bi ovaj postupak izostavio na školjci ali sada sam baš od neke volje da sve lipo raspišem.
Množenjem sa 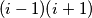 dobijamo
dobijamo
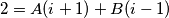 Sad uvrstimo
Sad uvrstimo 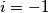 ( da bi se prvi član pokratio)
( da bi se prvi član pokratio) 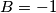 Sad uvrstavamo
Sad uvrstavamo 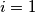 (da bi se drugi član pokratio)
(da bi se drugi član pokratio) 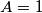 Znaći ovo su vrlo ljepa rješenja.
Znaći ovo su vrlo ljepa rješenja.
Sad imamo da je.
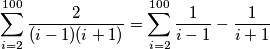
Idemo raspisati prvih par članova da vidimo kako se pokrati sve.
![\left[\frac{1}{1} - \frac{1}{3}\right] + \left[\frac{1}{2} - \frac{1}{4}\right] + \left[\frac{1}{3} - \frac{1}{5}\right] + ... + \left[\frac{1}{98} - \frac{1}{100}\right] + \left[\frac{1}{99} - \frac{1}{101}\right]](/media/m/7/3/b/73b72215baf454bf682316e3b14ffeff.png)
Sad nazovimo te parove 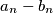 Primjetimo kako se
Primjetimo kako se 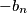 pokrati sa
pokrati sa 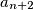 Sad pošto je
Sad pošto je 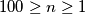 imamo da će ostati
imamo da će ostati 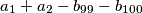
Tako da to je rezultat te sume
Rješenje je onda
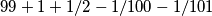
Kao prvo najbolje mi izgleda da izvućem jedinicu iz svakog razlomka na način :
$$\frac{a^2 + 1}{a^2 - 1} = 1 + \frac{2}{a^2 - 1}$$
Sad sve to mogu zapisat kao
$$99 + \sum_{i = 2}^{100} \frac{2}{(i - 1)(i + 1)}$$
Sad ovo je samo "teleskopiranje"
Tako da idemo rastavit na parcijalne razlomke.
$$\frac{2}{(i - 1)(i + 1)} = \frac{A}{i - 1} + \frac{B}{i + 1}$$
Obično bi ovaj postupak izostavio na školjci ali sada sam baš od neke volje da sve lipo raspišem.
Množenjem sa $(i - 1)(i + 1)$ dobijamo
$$2 = A(i + 1) + B(i - 1)$$
Sad uvrstimo $i = -1$ ( da bi se prvi član pokratio)
$$B = -1$$
Sad uvrstavamo $i = 1$ (da bi se drugi član pokratio)
$$A = 1$$
Znaći ovo su vrlo ljepa rješenja.
Sad imamo da je.
$$\sum_{i = 2}^{100} \frac{2}{(i - 1)(i + 1)} = \sum_{i = 2}^{100} \frac{1}{ i - 1} - \frac{1}{ i + 1}$$
Idemo raspisati prvih par članova da vidimo kako se pokrati sve.
$$\left[\frac{1}{1} - \frac{1}{3}\right] + \left[\frac{1}{2} - \frac{1}{4}\right] + \left[\frac{1}{3} - \frac{1}{5}\right] + ... + \left[\frac{1}{98} - \frac{1}{100}\right] + \left[\frac{1}{99} - \frac{1}{101}\right]$$
Sad nazovimo te parove $a_n - b_n$
Primjetimo kako se $-b_n$ pokrati sa $a_{n + 2}$
Sad pošto je $100 \geq n \geq 1$ imamo da će ostati
$$a_1 + a_2 - b_{99} - b_{100}$$
Tako da to je rezultat te sume
Rješenje je onda
$$99 + 1 + 1/2 - 1/100 - 1/101$$
| 7. prosinca 2022. 14:33 | iivan | Točno |
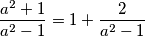
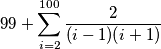
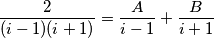
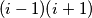 dobijamo
dobijamo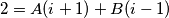 Sad uvrstimo
Sad uvrstimo 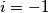 ( da bi se prvi član pokratio)
( da bi se prvi član pokratio) 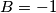 Sad uvrstavamo
Sad uvrstavamo 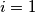 (da bi se drugi član pokratio)
(da bi se drugi član pokratio) 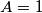 Znaći ovo su vrlo ljepa rješenja.
Znaći ovo su vrlo ljepa rješenja.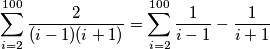
![\left[\frac{1}{1} - \frac{1}{3}\right] + \left[\frac{1}{2} - \frac{1}{4}\right] + \left[\frac{1}{3} - \frac{1}{5}\right] + ... + \left[\frac{1}{98} - \frac{1}{100}\right] + \left[\frac{1}{99} - \frac{1}{101}\right]](/media/m/7/3/b/73b72215baf454bf682316e3b14ffeff.png)
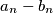 Primjetimo kako se
Primjetimo kako se 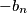 pokrati sa
pokrati sa 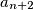 Sad pošto je
Sad pošto je 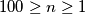 imamo da će ostati
imamo da će ostati 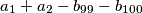
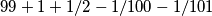
 Školjka
Školjka