Točno
7. prosinca 2022. 01:42 (3 godine, 2 mjeseci)
Dokažite da za svaka dva realna broja
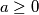
i
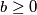
vrijedi nejednakost
![\frac{a + \sqrt[3]{a^2b} + \sqrt[3]{ab^2} + b}{4} \leq \frac{a + \sqrt{ab} + b}{3}\text{.}](/media/m/1/c/b/1cb6a951725f0cd08d9806c76d8ff355.png)
%V0
Dokažite da za svaka dva realna broja $a \geq 0$ i $b \geq 0$ vrijedi nejednakost $$\frac{a + \sqrt[3]{a^2b} + \sqrt[3]{ab^2} + b}{4} \leq \frac{a + \sqrt{ab} + b}{3}\text{.}$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Množimo sa $12$
$$4a + 4\sqrt{ab} + 4b \geq 3a + 3b + 3\sqrt[3]{a^2b} + 3\sqrt[3]{ab^2}$$
Pokratimo $3(a + b)$
$$a + 4\sqrt{ab} + b \geq 3\sqrt[3]{a^2b} + 3\sqrt[3]{ab^2}$$
Sad koristimo AG-nejednakost koja taman vrijedi za $a , b \geq 0$
$$\sqrt{ab} + \sqrt{ab} + a\geq 3\sqrt[3]{\sqrt{ab}^2 a}$$
$$\sqrt{ab} + \sqrt{ab} + b\geq 3\sqrt[3]{\sqrt{ab}^2 b}$$
I to kad se zbroji se dobije originalna nejednakost. Samo bez $3(a + b)$ al to lako dodamo kasnije.
| 7. prosinca 2022. 09:09 | 11235 | Točno |