Neocijenjeno
8. prosinca 2022. 01:37 (1 godina, 11 mjeseci)
Odredi: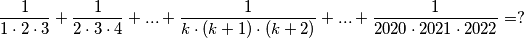 
Odredi: $$\frac{1}{1\cdot2\cdot3} + \frac{1}{2\cdot3\cdot4} + ... + \frac{1}{k\cdot(k+1)\cdot(k+2)} + ... + \frac{1}{2020\cdot2021\cdot2022} = ?$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
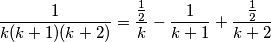
Zapisivajući samo prvih par brojeva mi govori sve
![\left[\frac{\frac{1}{2}}{1} - \frac{1}{2} + \frac{\frac{1}{2}}{3} \right] + \left[\frac{\frac{1}{2}}{2} - \frac{1}{3} + \frac{\frac{1}{2}}{4} \right] + \left[\frac{\frac{1}{2}}{3} - \frac{1}{4} + \frac{\frac{1}{2}}{5} \right]](/media/m/f/9/4/f94c19f8d3ab2850d6f9383c6d2b3b1c.png)
Ostat će uvijek 
zadnja dva i ovaj zadnji predzadnji.
Tjst
Rješenje je
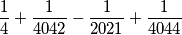
Koliko god da to je
$$\frac{1}{k(k +1)(k + 2) } = \frac{\frac{1}{2}}{k} -\frac{1}{k + 1} + \frac{\frac{1}{2}}{k + 2}$$
Zapisivajući samo prvih par brojeva mi govori sve
$$\left[\frac{\frac{1}{2}}{1} - \frac{1}{2} + \frac{\frac{1}{2}}{3} \right] + \left[\frac{\frac{1}{2}}{2} - \frac{1}{3} + \frac{\frac{1}{2}}{4} \right] + \left[\frac{\frac{1}{2}}{3} - \frac{1}{4} + \frac{\frac{1}{2}}{5} \right] $$
Ostat će uvijek $\frac{1}{4}$ zadnja dva i ovaj zadnji predzadnji.
Tjst
Rješenje je
$$\frac{1}{4} + \frac{1}{4042} - \frac{1}{2021} + \frac{1}{4044}$$
Koliko god da to je
Školjka