Točno
12. prosinca 2022. 23:37 (3 godine, 2 mjeseci)
Odredi sve realne brojeve \(x\) za koje vrijedi
\[
\left\lfloor \frac{x^2 + 1}{x + 2} \right\rfloor + \left\lfloor \frac{x - 1}{2} \right\rfloor = \frac{x(3x + 1)}{2(x + 2)}.
\]
\emph{Za realni broj \(t\), \(\lfloor t\rfloor\) je najveći cijeli broj koji nije veći od \(t\).
Na primjer, ako je \(t=3.14\), onda je \(\lfloor t \rfloor=3\).}
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Zbrajanjem dvije jednakosti 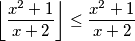
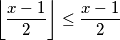
Dobijamo 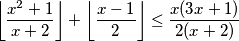
Iz ovoga i uvjeta zadatka imamo da mora biti slučaj nejednakosti a to se događa kada je
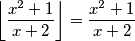
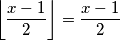
Ili ti broj ispod floor funkcije je već cijel. Ovu druga jednakost nam samo govori da je 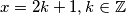
Tako da imamo
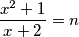 Gdje je
Gdje je 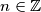
Djeljenjem polinoma imamo
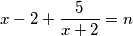
 je cijel tako da gledamo
je cijel tako da gledamo 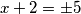
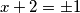
Odavde imamo 4 rješenja koja zadovoljavaju sve što se traži.
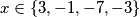 Valjda mogu ovako zapisat rješenje. Saznat ću valjda.
Valjda mogu ovako zapisat rješenje. Saznat ću valjda.
Zbrajanjem dvije jednakosti
$$\left\lfloor \frac{x^2 + 1}{x +2} \right\rfloor \leq \frac{x^2 + 1}{x + 2}$$
$$\left\lfloor \frac{x - 1}{2} \right\rfloor \leq \frac{x - 1}{2}$$
Dobijamo
$$\left\lfloor \frac{x^2 + 1}{x +2} \right\rfloor + \left\lfloor \frac{x - 1}{2} \right\rfloor \leq \frac{x(3x + 1)}{2(x + 2)}$$
Iz ovoga i uvjeta zadatka imamo da mora biti slučaj nejednakosti a to se događa kada je
$$\left\lfloor \frac{x^2 + 1}{x +2} \right\rfloor = \frac{x^2 + 1}{x + 2}$$
$$\left\lfloor \frac{x - 1}{2} \right\rfloor = \frac{x - 1}{2}$$
Ili ti broj ispod floor funkcije je već cijel. Ovu druga jednakost nam samo govori da je $x = 2k + 1 , k \in \mathbb{Z}$
Tako da imamo
$$\frac{x^2 + 1}{x + 2} = n$$
Gdje je $n \in \mathbb{Z}$
Djeljenjem polinoma imamo
$$x - 2 + \frac{5}{x + 2} = n$$
$x$ je cijel tako da gledamo
$$x + 2 = \pm 5$$
$$x + 2 = \pm 1$$
Odavde imamo 4 rješenja koja zadovoljavaju sve što se traži.
$$x \in \{3 , -1 , -7 , -3\}$$
Valjda mogu ovako zapisat rješenje. Saznat ću valjda.
| 13. prosinca 2022. 17:54 | iivan | Točno |
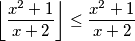
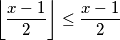
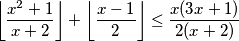
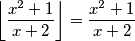
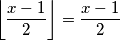
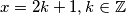
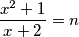 Gdje je
Gdje je 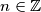
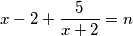
 je cijel tako da gledamo
je cijel tako da gledamo 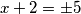
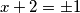
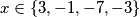 Valjda mogu ovako zapisat rješenje. Saznat ću valjda.
Valjda mogu ovako zapisat rješenje. Saznat ću valjda.  Školjka
Školjka  za koje vrijedi
za koje vrijedi 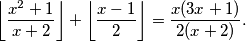
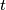 ,
, 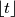 je najveći cijeli broj koji nije veći od
je najveći cijeli broj koji nije veći od 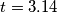 , onda je
, onda je 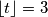 .
.