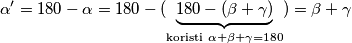Točno
14. prosinca 2022. 15:56 (3 godine, 2 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Povucemo pravac koja prolazi tockom C trokuta ABC, a paralelna je duzini AB. Prema pravilu kuta uz presjecnicu usporednih pravaca https://ibb.co/0DDPypz pa je zbroj kutova u trokutu ispruzeni kut tj, 180 stupnjeva.
Ako postavimo neku tocku unutar n-terokuta koja se ne nalazi na duzinama i povezemo svaki vrh tog n-terokuta s tom tockom, dobijemo n trokuta, svaki sa zbrojem kutova 180. No, uvijek ce preostati puni kut od 360 sa vrhom u toj tocki. 360=2*180. Tada je zbroj svih unutarnjih kutova tog n-terokuta n*180-180 = n*180-2*180 = (n-2)*180
npr. https://ibb.co/KW8wXGZ
 Školjka
Školjka  -terokuta jednak
-terokuta jednak 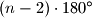 .
.