Točno
9. prosinca 2022. 21:53 (1 godina, 4 mjeseci)
U trokutu
vrijedi
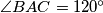
. Točka
nalazi se unutar trokuta tako da vrijedi
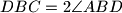
i
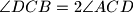
. Izračunaj mjeru kuta
.
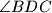
%V0
U trokutu $\triangle ABC$ vrijedi $\angle BAC = 120^{\circ}$. Točka $D$ nalazi se unutar trokuta tako da vrijedi $DBC = 2 \angle ABD$ i $\angle DCB = 2 \angle ACD$. Izračunaj mjeru kuta $\angle BDC$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
|∠ACD|=a i |∠CCB|=2a
|∠ABD|=a i |∠DBC|=2b
Kako je |∠BAC|=120, a+2a+b+2b=3a+3b = 180-120=60
3a+3b=60, tj. a+b=20
2a+2b=2*20=40 pa je |∠BDC|=180-40=140
|∠ACD|=a i |∠CCB|=2a\\
|∠ABD|=a i |∠DBC|=2b\\
Kako je |∠BAC|=120, a+2a+b+2b=3a+3b = 180-120=60\\
3a+3b=60, tj. a+b=20\\
2a+2b=2*20=40 pa je |∠BDC|=180-40=140
| 10. prosinca 2022. 02:11 | Patrlk | Točno |
| 13. prosinca 2022. 18:02 | iivan | Točno |
Školjka