Točno
14. prosinca 2022. 17:00 (3 godine, 2 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Vrijedi |OA|=|OB|=|OC| pa su trokuti △ABO, △BCO i △CAO jednakokracni.
Neka je |∠OCA| = |∠CAO| = γ, |∠OBA| = |∠BAO| = β, |∠OAD| = α, i |∠BAD| = δ
β = δ+α
Kako je △BDA pravokutan, |∠OBC| = 180-90-β-δ = 90-(δ+α)-δ = 90-2δ-α
△DCA je takoder pravokutan pa je |∠BCO| = 180-90-2γ-α = 90-2γ-α
Dakle kako je |∠OBC| = |∠BCO| (zbog jednakokracnog trokuta): // 90-2δ-α = 90-2γ-α
2δ = 2γ pa δ=γ, tj. |∠BAD| = |∠CAO|
 Školjka
Školjka  središte opisane kružnice, a
središte opisane kružnice, a  nožište visine na
nožište visine na  u trokutu
u trokutu  . Dokažite
. Dokažite 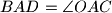 .
.