Točno
19. prosinca 2022. 13:05 (3 godine, 2 mjeseci)
Let  be an isosceles triangle with
be an isosceles triangle with 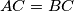 , whose incentre is
, whose incentre is  . Let
. Let  be a point on the circumcircle of the triangle
be a point on the circumcircle of the triangle 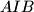 lying inside the triangle
lying inside the triangle  . The lines through
. The lines through  parallel to
parallel to  and
and 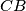 meet
meet  at
at  and
and  , respectively. The line through
, respectively. The line through  parallel to
parallel to  meets
meets  and
and 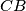 at
at  and
and  , respectively. Prove that the lines
, respectively. Prove that the lines 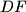 and
and 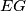 intersect on the circumcircle of the triangle
intersect on the circumcircle of the triangle  .
.
comment
(According to my team leader, last year some of the countries wanted a geometry question that was even easier than this...that explains IMO 2003/4...)
[Note by Darij: This was also Problem 6 of the German pre-TST 2004, written in December 03.]
Edited by Orl.
 be an isosceles triangle with
be an isosceles triangle with 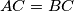 , whose incentre is
, whose incentre is  . Let
. Let  be a point on the circumcircle of the triangle
be a point on the circumcircle of the triangle 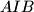 lying inside the triangle
lying inside the triangle  . The lines through
. The lines through  parallel to
parallel to  and
and 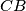 meet
meet  at
at  and
and  , respectively. The line through
, respectively. The line through  parallel to
parallel to  meets
meets  and
and 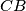 at
at  and
and  , respectively. Prove that the lines
, respectively. Prove that the lines 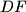 and
and 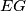 intersect on the circumcircle of the triangle
intersect on the circumcircle of the triangle  .
. comment
(According to my team leader, last year some of the countries wanted a geometry question that was even easier than this...that explains IMO 2003/4...)
[Note by Darij: This was also Problem 6 of the German pre-TST 2004, written in December 03.]
Edited by Orl.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Neka je  presjek
presjek 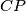 i
i  . Dokazat ćemo da je
. Dokazat ćemo da je  na
na 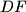 i na
i na 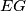 . (Motivacija za to je činjenica da su
. (Motivacija za to je činjenica da su 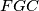 i
i 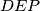 homotetični pa se
homotetični pa se 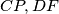 i
i 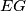 sijeku u jednoj točki, pa ako zadatak vrijedi to će morati biti traženi presjek.)
sijeku u jednoj točki, pa ako zadatak vrijedi to će morati biti traženi presjek.)
Zbog simetrije dovoljno je da je  na
na 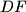 . Imamo:
. Imamo: 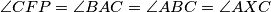 , odakle je
, odakle je 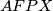 tetivan, a kako je
tetivan, a kako je 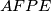 jednakokračni trapez i
jednakokračni trapez i  leži na toj kružnici. Sličan chase daje i tetivnost
leži na toj kružnici. Sličan chase daje i tetivnost 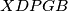 . Sada,
. Sada, 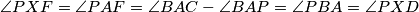 što smo i trebali.
što smo i trebali.
P.S. Dosta lagano za jedan G5, nakon nacrtane slike mislim da se i bez ovog argumenta homotetijom može naslutiti gdje će biti ta točka presjeka i od tamo je chase dosta lagan. Ako se usmjere kutevi može se dobiti da zadatak vrijedi i za  izvan
izvan 
 Školjka
Školjka