Točno
23. prosinca 2022. 15:59 (3 godine, 2 mjeseci)
Neka se točke

i

nalaze redom na stranicama

i

trokuta

. Simetrale kutova
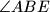
i
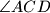
sijeku se u točki

. Dokažite da je
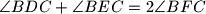
.
%V0
Neka se točke $D$ i $E$ nalaze redom na stranicama $AB$ i $AC$ trokuta $ABC$. Simetrale kutova $\angle ABE$ i $\angle ACD$ sijeku se u točki $F$. Dokažite da je $\angle BDC + \angle BEC = 2 \angle BFC$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Oznacimo |∠ABF|=|∠FBE|=β' i |∠EBC|=β. |∠DCF|=|∠FCE|=γ' i |∠BCD|=γ. |∠BEC|=x, |∠BFC|=y i |∠BDC|=z.
Iz trokuta BCD dobijemo z+γ+β+2β' = 180
Iz trokuta BCF, y+γ+γ'+β+β' = 180
Iz trokuta BCE x+2γ'+β+γ = 180
y+γ+γ'+β+β' - z+γ+β+2β' = 180-180 = 0, tj. y-z+γ'-β' = 0
y+γ+γ'+β+β' - x+2γ'+β+γ = 180-180 = 0, tj. y-x-γ'+β' = 0
Kako obje jednakosti vrijede 0, mozemo ih oduzeti i dobiti, y-z+γ'-β' - y-x-γ'+β' = 0, 2y-z-x = 0, tj. 2y=z+x
z+x=2y ili |∠BDC|+|∠BEC|=2|∠BFC|
Oznacimo |∠ABF|=|∠FBE|=β' i |∠EBC|=β. |∠DCF|=|∠FCE|=γ' i |∠BCD|=γ. |∠BEC|=x, |∠BFC|=y i |∠BDC|=z. \\
Iz trokuta BCD dobijemo z+γ+β+2β' = 180 \\
Iz trokuta BCF, y+γ+γ'+β+β' = 180 \\
Iz trokuta BCE x+2γ'+β+γ = 180 \\
y+γ+γ'+β+β' - z+γ+β+2β' = 180-180 = 0, tj. y-z+γ'-β' = 0 \\
y+γ+γ'+β+β' - x+2γ'+β+γ = 180-180 = 0, tj. y-x-γ'+β' = 0 \\
Kako obje jednakosti vrijede 0, mozemo ih oduzeti i dobiti, y-z+γ'-β' - y-x-γ'+β' = 0, 2y-z-x = 0, tj. 2y=z+x \\
z+x=2y ili |∠BDC|+|∠BEC|=2|∠BFC|
| 30. prosinca 2022. 16:45 | iivan | Točno |
 Školjka
Školjka  i
i  nalaze redom na stranicama
nalaze redom na stranicama  i
i  trokuta
trokuta  . Simetrale kutova
. Simetrale kutova 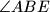 i
i 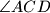 sijeku se u točki
sijeku se u točki  . Dokažite da je
. Dokažite da je 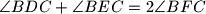 .
.