Točno
29. prosinca 2022. 13:54 (1 godina, 4 mjeseci)
Ako je zbroj kvadrata triju prostih brojeva
,
,
prost broj, dokaži da je barem jedan od brojeva
,
,
jednak
.
%V0
Ako je zbroj kvadrata triju prostih brojeva $a$, $b$, $c$ prost broj, dokaži da je barem jedan od brojeva $a$, $b$, $c$ jednak $3$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
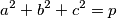Zamislimo da niti jedan od a , b ,c nije . Onda kad gledamo ostatke; p mora biti 3. A to je nemoguće jer zbroj nikoja 3 kvadrata prostih brojeva nije 3.
$$a^2 + b^2 + c^2 = p$$
Zamislimo da niti jedan od a , b ,c nije $3$.
Onda kad gledamo ostatke; p mora biti 3. A to je nemoguće jer zbroj nikoja 3 kvadrata prostih brojeva nije 3.
Školjka