Neocijenjeno
24. prosinca 2022. 02:16 (2 godine, 2 mjeseci)
Pravac
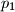
presijeca graf kvadratne funkcije
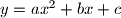
u točkama
i
. Pravac
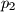
paralelan je pravcu
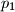
i presijeca isti graf u točkama
i
. Dokaži da je suma apscisa točaka
i
jednaka sumi apscisa točaka
i
.
%V0
Pravac $p_1$ presijeca graf kvadratne funkcije $y=ax^2+bx+c$ u točkama $A$ i $B$. Pravac $p_2$ paralelan je pravcu $p_1$ i presijeca isti graf u točkama $C$ i $D$. Dokaži da je suma apscisa točaka $A$ i $B$ jednaka sumi apscisa točaka $C$ i $D$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Zamislimo dvije jednađbe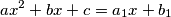 
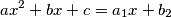
Prema vietovoj formuli zbroj apscisa (zbroj rješenja tih jednađbi) je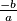 
A to se nece promjenit samo zato sto smo nesto mjenjali 
Zamislimo dvije jednađbe
$$ax^2 + bx + c = a_1x + b_1$$
$$ax^2 + bx + c = a_1x + b_2$$
Prema vietovoj formuli zbroj apscisa (zbroj rješenja tih jednađbi) je $\frac{-b}{a}$
A to se nece promjenit samo zato sto smo nesto mjenjali $c$
Školjka