Neocijenjeno
7. rujna 2023. 22:41 (1 godina, 6 mjeseci)
Neka su
i
prirodni brojevi,
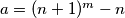
i
.
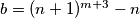
Dokažite da su
i
relativno prosti ako
nije djeljiv s
.
Odredite sve brojeve
i
za koje
i
nisu relativno prosti.
%V0
Neka su $m$ i $n$ prirodni brojevi, $a = (n+1)^m - n$ i $b = (n+1)^{m+3} - n$.
$(a)$ Dokažite da su $a$ i $b$ relativno prosti ako $m$ nije djeljiv s $3$.
$(b)$ Odredite sve brojeve $m$ i $n$ za koje $a$ i $b$ nisu relativno prosti.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Ok znaci radimo puno euklidovog algoritma dok ne dođemo do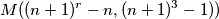 
r je m mod 3 Dokažemo da m = 1 , 2 ne radi
I za m = 3k , n = 7k +1 a , b su djeljivi sa 7
Ok znaci radimo puno euklidovog algoritma dok ne dođemo do
$$M((n + 1)^r - n , (n + 1)^3 - 1))$$
r je m mod 3
Dokažemo da m = 1 , 2 ne radi
I za m = 3k , n = 7k +1
a , b su djeljivi sa 7
Školjka