pekipecmalizec, 18. siječnja 2023. 20:40
Mislim da ti nije dobro. Dokazao si da je LHS >= 9 sto je okej, ali si dokazao i da je RHS >= 9, pa ne mozes tvrditi da vrijedi LHS >= RHS. Obicno bi trebao dobit nesto tipa LHS >= neki izraz >= RHS. Ja inace razmisljam na nacin da ako trebam dokazat da je neki izraz A veci od nekog izraza B, mogu povecati izraz B (ili smanjit A) i ako onda uspijem dokazati rijesio sam zadatak. Ako dokazujes da je izraz A veci od izraza B, ne smijes povecavati A ili smanjivati B jer ako nakon toga dobijes da je A >= B neces moc tvrdit da je pocetni A bio veci od pocetnog B.
Nadam se da si skuzio kaj zelim rec i ak si skuzio nadam se da ti je pomoglo. Iako moguce je i da sam se ja zeznuo jer sam pospan mogo bi neki power nap nabacit.
Hvala
[quote]Mislim da ti nije dobro. Dokazao si da je LHS >= 9 sto je okej, ali si dokazao i da je RHS >= 9, pa ne mozes tvrditi da vrijedi LHS >= RHS. Obicno bi trebao dobit nesto tipa LHS >= neki izraz >= RHS. Ja inace razmisljam na nacin da ako trebam dokazat da je neki izraz A veci od nekog izraza B, mogu povecati izraz B (ili smanjit A) i ako onda uspijem dokazati rijesio sam zadatak. Ako dokazujes da je izraz A veci od izraza B, ne smijes povecavati A ili smanjivati B jer ako nakon toga dobijes da je A >= B neces moc tvrdit da je pocetni A bio veci od pocetnog B.
Nadam se da si skuzio kaj zelim rec i ak si skuzio nadam se da ti je pomoglo. Iako moguce je i da sam se ja zeznuo jer sam pospan mogo bi neki power nap nabacit.[/quote]
Hvala
fini_keksi, 12. siječnja 2023. 18:21
Mislim da ti nije dobro. Dokazao si da je LHS >= 9 sto je okej, ali si dokazao i da je RHS >= 9, pa ne mozes tvrditi da vrijedi LHS >= RHS. Obicno bi trebao dobit nesto tipa LHS >= neki izraz >= RHS. Ja inace razmisljam na nacin da ako trebam dokazat da je neki izraz A veci od nekog izraza B, mogu povecati izraz B (ili smanjit A) i ako onda uspijem dokazati rijesio sam zadatak. Ako dokazujes da je izraz A veci od izraza B, ne smijes povecavati A ili smanjivati B jer ako nakon toga dobijes da je A >= B neces moc tvrdit da je pocetni A bio veci od pocetnog B.
Nadam se da si skuzio kaj zelim rec i ak si skuzio nadam se da ti je pomoglo. Iako moguce je i da sam se ja zeznuo jer sam pospan mogo bi neki power nap nabacit.
Mislim da ti nije dobro. Dokazao si da je LHS >= 9 sto je okej, ali si dokazao i da je RHS >= 9, pa ne mozes tvrditi da vrijedi LHS >= RHS. Obicno bi trebao dobit nesto tipa LHS >= neki izraz >= RHS. Ja inace razmisljam na nacin da ako trebam dokazat da je neki izraz A veci od nekog izraza B, mogu povecati izraz B (ili smanjit A) i ako onda uspijem dokazati rijesio sam zadatak. Ako dokazujes da je izraz A veci od izraza B, ne smijes povecavati A ili smanjivati B jer ako nakon toga dobijes da je A >= B neces moc tvrdit da je pocetni A bio veci od pocetnog B.
Nadam se da si skuzio kaj zelim rec i ak si skuzio nadam se da ti je pomoglo. Iako moguce je i da sam se ja zeznuo jer sam pospan mogo bi neki power nap nabacit.
pekipecmalizec, 10. siječnja 2023. 19:13
Na desnoj strani nejednakosti iskoristio sam AG nejednakost i onda je
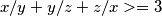
Trebam dokazati da je nejednakost veća od 9. Raspisati ću lijevu stanu nejednakosti kao
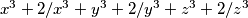
Ako uparim
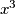
i
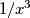
i iskoristim AG nejednakost dobit ću da je to veće ili jednako 2. To isto napravim za
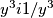
i za
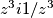
ostane mi
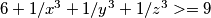
To jest
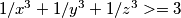
I sada opet iskoristim AG nejednakost I dobijem da je lijeva strana nejednakosti veća ili jednaka od trećeg korijena iz
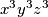
a kako je xyz=1 onda je i treći korijen iz
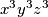
jednak 1 pa je 3>=3. Može li mi netko provjeriti rjesenje? Hvala.
Zabunio sam se umjesto treći korijen iz
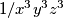
sam napisao treći korijen iz
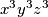
[quote]Na desnoj strani nejednakosti iskoristio sam AG nejednakost i onda je $x/y+y/z+z/x>=3$
Trebam dokazati da je nejednakost veća od 9.
Raspisati ću lijevu stanu nejednakosti kao $x^3+ 2/x^3+y^3+2/y^3+z^3+2/z^3$
Ako uparim $x^3$ i $1/x^3$ i iskoristim AG nejednakost dobit ću da je to veće ili jednako 2.
To isto napravim za $y^3 i 1/y^3$ i za $z^3 i 1/z^3$ ostane mi $6+1/x^3+1/y^3+1/z^3>=9$
To jest $1/x^3+1/y^3+1/z^3>=3$
I sada opet iskoristim AG nejednakost I dobijem da je lijeva strana nejednakosti veća ili jednaka od trećeg korijena iz $x^3y^3z^3$ a kako je xyz=1 onda je i treći korijen iz $x^3y^3z^3$ jednak 1 pa je 3>=3.
Može li mi netko provjeriti rjesenje? Hvala.[/quote]
Zabunio sam se umjesto treći korijen iz $1/x^3y^3z^3$ sam napisao treći korijen iz $x^3y^3z^3$
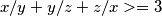 Trebam dokazati da je nejednakost veća od 9. Raspisati ću lijevu stanu nejednakosti kao
Trebam dokazati da je nejednakost veća od 9. Raspisati ću lijevu stanu nejednakosti kao 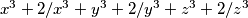 Ako uparim
Ako uparim 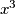 i
i 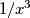 i iskoristim AG nejednakost dobit ću da je to veće ili jednako 2. To isto napravim za
i iskoristim AG nejednakost dobit ću da je to veće ili jednako 2. To isto napravim za 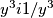 i za
i za 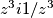 ostane mi
ostane mi 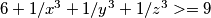 To jest
To jest 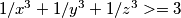 I sada opet iskoristim AG nejednakost I dobijem da je lijeva strana nejednakosti veća ili jednaka od trećeg korijena iz
I sada opet iskoristim AG nejednakost I dobijem da je lijeva strana nejednakosti veća ili jednaka od trećeg korijena iz 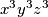 a kako je xyz=1 onda je i treći korijen iz
a kako je xyz=1 onda je i treći korijen iz 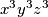 jednak 1 pa je 3>=3. Može li mi netko provjeriti rjesenje? Hvala.
jednak 1 pa je 3>=3. Može li mi netko provjeriti rjesenje? Hvala. 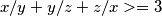 Trebam dokazati da je nejednakost veća od 9. Raspisati ću lijevu stanu nejednakosti kao
Trebam dokazati da je nejednakost veća od 9. Raspisati ću lijevu stanu nejednakosti kao 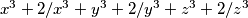 Ako uparim
Ako uparim 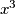 i
i 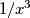 i iskoristim AG nejednakost dobit ću da je to veće ili jednako 2. To isto napravim za
i iskoristim AG nejednakost dobit ću da je to veće ili jednako 2. To isto napravim za 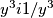 i za
i za 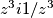 ostane mi
ostane mi 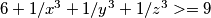 To jest
To jest 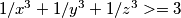 I sada opet iskoristim AG nejednakost I dobijem da je lijeva strana nejednakosti veća ili jednaka od trećeg korijena iz
I sada opet iskoristim AG nejednakost I dobijem da je lijeva strana nejednakosti veća ili jednaka od trećeg korijena iz 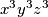 a kako je xyz=1 onda je i treći korijen iz
a kako je xyz=1 onda je i treći korijen iz 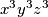 jednak 1 pa je 3>=3. Može li mi netko provjeriti rjesenje? Hvala.
jednak 1 pa je 3>=3. Može li mi netko provjeriti rjesenje? Hvala.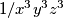 sam napisao treći korijen iz
sam napisao treći korijen iz 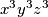
 Školjka
Školjka  ,
,  i
i  pozitivni realni brojevi za koje vrijedi
pozitivni realni brojevi za koje vrijedi 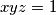 . Dokaži nejednakost
. Dokaži nejednakost