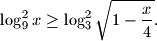Prvo moramo paziti na uvjete logaritmanda, tj. vrijedi: 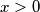 i
i 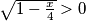 . Rješenje prvog uvjeta (nejednadžbe) je
. Rješenje prvog uvjeta (nejednadžbe) je 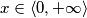 , a drugog uvjeta (nejednadžbe) je
, a drugog uvjeta (nejednadžbe) je 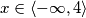 . Dakle, promatramo x iz intervala
. Dakle, promatramo x iz intervala 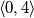 .
. 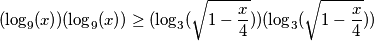
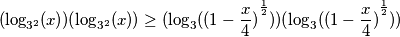
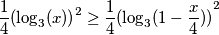
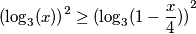 Sad možemo sve korjenovati, pazeći na apsolutnu vrijednost:
Sad možemo sve korjenovati, pazeći na apsolutnu vrijednost: 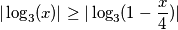
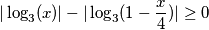 Odredimo nul - točke:
Odredimo nul - točke: 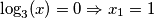 i
i 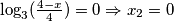 . Imamo tri slučaja, ovisno o predznacima:
. Imamo tri slučaja, ovisno o predznacima:
1° Ako je 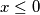 , nije potrebno promatrati. Zbog početnog uvjeta (logaritmanda) nema smisla promatrati ovaj slučaj.
, nije potrebno promatrati. Zbog početnog uvjeta (logaritmanda) nema smisla promatrati ovaj slučaj.
2° Ako je ![x \in \langle 0, 1 ]](/media/m/d/5/2/d52411d9ea1ae4c2639e9f4ab37ccd8b.png) :
:
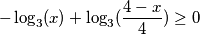
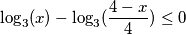
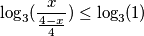
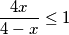
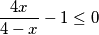
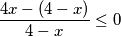
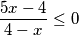
Rješenje ove nejednadžbe ![x \in \langle -\infty, \frac {4} {5}] \cup \langle 4 +\infty \rangle](/media/m/b/d/0/bd0501dc3eef5cda52208e0fd7f27cec.png) . Naravno, promatramo samo
. Naravno, promatramo samo ![x \in \langle 0, 1 ]](/media/m/d/5/2/d52411d9ea1ae4c2639e9f4ab37ccd8b.png) , dakle, rješenje ovog slučaja je
, dakle, rješenje ovog slučaja je ![x \in \langle 0,\frac {4} {5}]](/media/m/0/1/a/01a44f85ff2b3f18179cf28201450037.png) .
.
3° Ako je 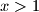 :
:
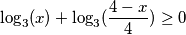
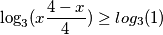
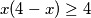
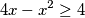
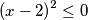 Ova nejednadžba ima samo rješenje
Ova nejednadžba ima samo rješenje 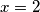 , koje pripada intervalu, u kojem smo promatrali ovaj slučaj.
, koje pripada intervalu, u kojem smo promatrali ovaj slučaj.
Unija svih slučajeva, tj. rješenje nejednadžbe (ujedno i rješenje zadatka) je ![x\in\langle0,\frac 4 5] \cup \{ 2 \}](/media/m/6/5/e/65e20b14f9e6b41e0aebad637a194972.png) . (Naravno, pazimo i na početni uvjet!)
. (Naravno, pazimo i na početni uvjet!)
Prvo moramo paziti na uvjete logaritmanda, tj. vrijedi: $ x>0 $ i $ \sqrt {1-\frac x 4} > 0 $. Rješenje prvog uvjeta (nejednadžbe) je $x \in \langle 0, +\infty \rangle$, a drugog uvjeta (nejednadžbe) je $x \in \langle -\infty, 4 \rangle$. Dakle, promatramo x iz intervala $\langle 0, 4 \rangle$.
$$(\log_9(x))(\log_9(x))\geq(\log_3(\sqrt {1-\frac x 4} ))(\log_3(\sqrt {1-\frac x 4} ))$$
$$(\log_{{3}^{2}}(x))(\log_{{3}^{2}}(x))\geq(\log_3({(1-\frac x 4)}^{\frac 1 2} ))(\log_3({(1-\frac x 4)}^{\frac 1 2}))$$
$$\frac 1 4 {(\log_3(x))}^{2} \geq \frac 1 4 {(\log_3(1-\frac x 4))}^{2}$$
$$ {(\log_3(x))}^{2} \geq {(\log_3(1-\frac x 4))}^{2}$$
Sad možemo sve korjenovati, pazeći na apsolutnu vrijednost:
$$|\log_3(x)| \geq |\log_3(1-\frac x 4)|$$
$$|\log_3(x)| - |\log_3(1-\frac x 4)|\geq 0$$
Odredimo nul - točke: $\log_3(x) = 0 \Rightarrow x_1 = 1$ i $\log_3(\frac {4-x} 4) = 0 \Rightarrow x_2 =0 $. Imamo tri slučaja, ovisno o predznacima:\\
1° Ako je $ x \le 0$, nije potrebno promatrati. Zbog početnog uvjeta (logaritmanda) nema smisla promatrati ovaj slučaj. \\
2° Ako je $ x \in \langle 0, 1 ]$:\\
$$ -\log_3(x) + \log_3(\frac {4-x} 4) \geq 0$$
$$ \log_3(x) - \log_3(\frac {4-x} 4) \leq 0 $$
$$ \log_3(\frac{x}{\frac {4-x} 4}) \leq \log_3(1) $$
$$ \frac {4x}{4-x} \leq 1 $$
$$ \frac {4x}{4-x}-1 \leq 0 $$
$$ \frac {4x-(4-x)} {4-x} \leq 0 $$
$$ \frac {5x-4} {4-x} \leq 0 $$ \\
Rješenje ove nejednadžbe $ x \in \langle -\infty, \frac {4} {5}] \cup \langle 4 +\infty \rangle $.
Naravno, promatramo samo $ x \in \langle 0, 1 ]$, dakle, rješenje ovog slučaja je $ x \in \langle 0,\frac {4} {5}]$.\\
3° Ako je $ x > 1$:\\
$$ \log_3(x) + \log_3(\frac {4-x} 4) \geq 0$$
$$ \log_3(x\frac{4-x}{4}) \geq log_3(1)$$
$$ x(4-x) \geq 4$$
$$ 4x-{x}^{2} \geq 4 $$
$$ {(x-2)}^{2} \leq 0$$
Ova nejednadžba ima samo rješenje $x=2$, koje pripada intervalu, u kojem smo promatrali ovaj slučaj.\\
Unija svih slučajeva, tj. rješenje nejednadžbe (ujedno i rješenje zadatka) je $x\in\langle0,\frac 4 5] \cup \{ 2 \}$. (Naravno, pazimo i na početni uvjet!)
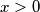 i
i 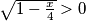 . Rješenje prvog uvjeta (nejednadžbe) je
. Rješenje prvog uvjeta (nejednadžbe) je 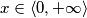 , a drugog uvjeta (nejednadžbe) je
, a drugog uvjeta (nejednadžbe) je 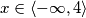 . Dakle, promatramo x iz intervala
. Dakle, promatramo x iz intervala 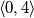 .
. 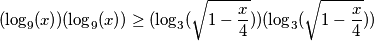
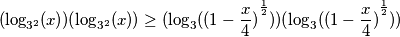
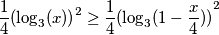
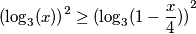 Sad možemo sve korjenovati, pazeći na apsolutnu vrijednost:
Sad možemo sve korjenovati, pazeći na apsolutnu vrijednost: 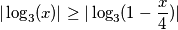
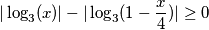 Odredimo nul - točke:
Odredimo nul - točke: 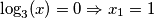 i
i 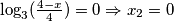 . Imamo tri slučaja, ovisno o predznacima:
. Imamo tri slučaja, ovisno o predznacima: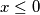 , nije potrebno promatrati. Zbog početnog uvjeta (logaritmanda) nema smisla promatrati ovaj slučaj.
, nije potrebno promatrati. Zbog početnog uvjeta (logaritmanda) nema smisla promatrati ovaj slučaj. ![x \in \langle 0, 1 ]](/media/m/d/5/2/d52411d9ea1ae4c2639e9f4ab37ccd8b.png) :
: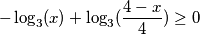
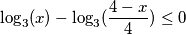
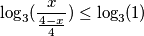
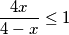
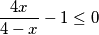
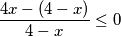
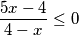
![x \in \langle -\infty, \frac {4} {5}] \cup \langle 4 +\infty \rangle](/media/m/b/d/0/bd0501dc3eef5cda52208e0fd7f27cec.png) . Naravno, promatramo samo
. Naravno, promatramo samo ![x \in \langle 0, 1 ]](/media/m/d/5/2/d52411d9ea1ae4c2639e9f4ab37ccd8b.png) , dakle, rješenje ovog slučaja je
, dakle, rješenje ovog slučaja je ![x \in \langle 0,\frac {4} {5}]](/media/m/0/1/a/01a44f85ff2b3f18179cf28201450037.png) .
.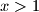 :
: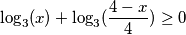
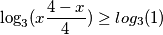
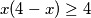
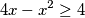
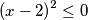 Ova nejednadžba ima samo rješenje
Ova nejednadžba ima samo rješenje 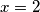 , koje pripada intervalu, u kojem smo promatrali ovaj slučaj.
, koje pripada intervalu, u kojem smo promatrali ovaj slučaj.![x\in\langle0,\frac 4 5] \cup \{ 2 \}](/media/m/6/5/e/65e20b14f9e6b41e0aebad637a194972.png) . (Naravno, pazimo i na početni uvjet!)
. (Naravno, pazimo i na početni uvjet!)  Školjka
Školjka