Neocijenjeno
8. kolovoza 2024. 17:18 (1 godina, 6 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Prvo moramo napisati uvjete za logaritmande:
1. 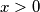
2. 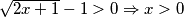
3. 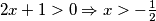
Dakle, promatramo  iz intervala
iz intervala 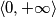 .
. 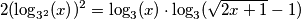
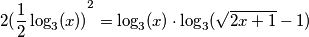
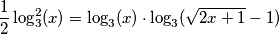 (Pazi! Ne krati jednadžbu s
(Pazi! Ne krati jednadžbu s 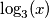 jer ga možeš izlučiti.)
jer ga možeš izlučiti.)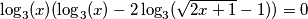 Imamo jednadžbu oblika
Imamo jednadžbu oblika 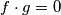 , koju rješavamo da svaki od faktora (
, koju rješavamo da svaki od faktora (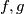 ) izjednačimo s nulom jer će tada umnožak biti jednak nuli.
) izjednačimo s nulom jer će tada umnožak biti jednak nuli.
1. (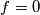 )
)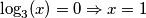 2. (
2. (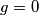 )
)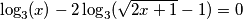
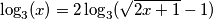
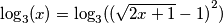
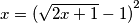 Pojednostavljivanjem došli smo do iracionalne jednadžbe čija je rješenja potrebno provjeriti (uvrštavanjem u početnu!)
Pojednostavljivanjem došli smo do iracionalne jednadžbe čija je rješenja potrebno provjeriti (uvrštavanjem u početnu!) 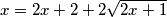
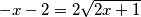
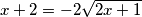 Promotrimo dobivenu jednadžbu. Ako je početni uvjet
Promotrimo dobivenu jednadžbu. Ako je početni uvjet 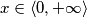 , tada je vrijednost
, tada je vrijednost 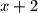 uvijek pozitivna. S druge strane jednakosti, možemo primijetiti sličnost;
uvijek pozitivna. S druge strane jednakosti, možemo primijetiti sličnost; 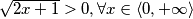 . Ali ispada da je pozitivna (lijeva) strana jednaka negativnoj (desnoj strani) za navedene
. Ali ispada da je pozitivna (lijeva) strana jednaka negativnoj (desnoj strani) za navedene  , što nije moguće. Dakle, navedena jednadžba, nema rješenja. Jedino rješenje jednadžbe je
, što nije moguće. Dakle, navedena jednadžba, nema rješenja. Jedino rješenje jednadžbe je  .
.
 Školjka
Školjka