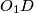Neka je  presjek
presjek  i
i 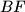 ,
,  centar
centar  , te neka je
, te neka je  presjek tangenti na
presjek tangenti na  kroz
kroz  i
i  . Također neka su
. Također neka su 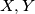 presjeci
presjeci  i
i  .
.
 :
:  je na
je na 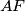 , analogno i na
, analogno i na 
Dokaz: Gledajmo homotetiju koja šalje  u
u  . Centar joj je
. Centar joj je  , a
, a  se šalje u polovište luka
se šalje u polovište luka  s druge strane
s druge strane  od
od  , što je upravo
, što je upravo  . Analogno je
. Analogno je  na
na  .
.
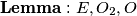 kolinearne, analogno
kolinearne, analogno 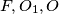 .
.
Dokaz: ista homotetija, centri kružnica se šalju jedan u drugi
 :
:  je na
je na  .
.
Dokaz: Uočimo da je  radikalno središte
radikalno središte 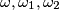
 : Trokuti
: Trokuti  i
i 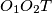 su homotetični
su homotetični
Dokaz: Kako je 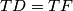 ,
, 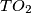 je simetrala
je simetrala 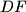 , stoga
, stoga 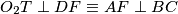 . Analogno je
. Analogno je 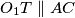 . Na kraju,
. Na kraju, 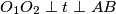 , pa su odgovarajuće stranice paralelne i to povlači našu tvrdnju.
, pa su odgovarajuće stranice paralelne i to povlači našu tvrdnju.
Ovo nam daje da su 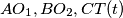 konkurentni. Cilj nam je pokazati da se ovom homotetijom i pravac
konkurentni. Cilj nam je pokazati da se ovom homotetijom i pravac  šalje u sebe. Zato neka je
šalje u sebe. Zato neka je  presjek
presjek  i
i 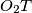 , dovoljno je pokazati da je
, dovoljno je pokazati da je 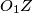 visina u
visina u 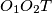 , odnosno
, odnosno 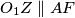 jer će tada
jer će tada 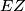 prolaziti kroz centar homotetije, odnosno dokazat ćemo zadatak. Još malo i gotovi smo, dokazat ćemo da su
prolaziti kroz centar homotetije, odnosno dokazat ćemo zadatak. Još malo i gotovi smo, dokazat ćemo da su 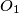 i
i  jednako udaljeni od
jednako udaljeni od 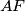 . Neka su
. Neka su 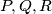 redom nožišta okomica iz
redom nožišta okomica iz 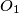 na
na 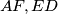 , te nožište okomice iz
, te nožište okomice iz  na
na 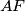
. Imamo: 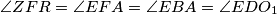 pa su
pa su 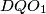 i
i 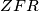 slični s koeficijentom sličnosti
slični s koeficijentom sličnosti 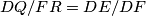 . Konačno,
. Konačno, 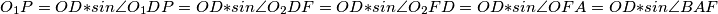
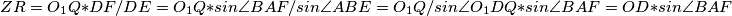 , što rješava.
, što rješava.
P.S.: Čini mi se da je glavna težina zadatka gledati zadatak iz konteksta  i dodavanje točke
i dodavanje točke  . Također, uvijek ako imate neke uvjete na tangentne kružnice, razmislite o homotetiji kao načinu za dokazivanje konkurentnosti (još pogotovo nakon ovih početnih lemica). Zadnji se dio može činiti ružan, ali meni je on bio najlakši jer sam već shvatio ove gore lemme i stvar je bila samo chaseanja i lagane trigonometrije. Za ljubitelje projektivne geometrije, u službenom shortlist paketu ima elegantan završetak Pappusom nakon što se dobije konkurentnost prva 3 pravca, pa koga zanima može pogledati. Također, ako netko ima nekih pitanja može se javiti u komentare, postoji solidna šansa da sam napravio zatipak negdje pa ću popraviti kad budem vidio.
. Također, uvijek ako imate neke uvjete na tangentne kružnice, razmislite o homotetiji kao načinu za dokazivanje konkurentnosti (još pogotovo nakon ovih početnih lemica). Zadnji se dio može činiti ružan, ali meni je on bio najlakši jer sam već shvatio ove gore lemme i stvar je bila samo chaseanja i lagane trigonometrije. Za ljubitelje projektivne geometrije, u službenom shortlist paketu ima elegantan završetak Pappusom nakon što se dobije konkurentnost prva 3 pravca, pa koga zanima može pogledati. Također, ako netko ima nekih pitanja može se javiti u komentare, postoji solidna šansa da sam napravio zatipak negdje pa ću popraviti kad budem vidio.
Neka je $C$ presjek $AE$ i $BF$, $O$ centar $\omega$, te neka je $T$ presjek tangenti na $\omega$ kroz $E$ i $F$. Također neka su $X,Y$ presjeci $t$ i $\omega$. \\
$\bold{Lemma}$: $D$ je na $AF$, analogno i na $BE$\\
Dokaz: Gledajmo homotetiju koja šalje $\omega_2$ u $\omega$. Centar joj je $F$, a $D$ se šalje u polovište luka $XY$ s druge strane $XY$ od $F$, što je upravo $A$. Analogno je $D$ na
$BE$.\\
$\bold{Lemma}:E, O_2, O$ kolinearne, analogno $F, O_1, O$.\\
Dokaz: ista homotetija, centri kružnica se šalju jedan u drugi\\
$\bold{Lemma}$: $T$ je na $t$.\\
Dokaz: Uočimo da je $T$ radikalno središte $\omega, \omega_1, \omega_2$\\
$\bold{Lemma}$: Trokuti $ABC$ i $O_1O_2T$ su homotetični\\
Dokaz: Kako je $TD=TF$, $TO_2$ je simetrala $DF$, stoga $O_2T \perp DF \equiv AF \perp BC$. Analogno je $O_1T \parallel AC$ . Na kraju,
$O_1O_2 \perp t \perp AB$ , pa su odgovarajuće stranice paralelne i to povlači našu tvrdnju. \\
\\
Ovo nam daje da su $AO_1, BO_2, CT(t)$ konkurentni. Cilj nam je pokazati da se ovom homotetijom i pravac $EF$ šalje u sebe. Zato neka je $Z$ presjek $EF$ i $O_2T$, dovoljno je pokazati da je $O_1Z$ visina u $O_1O_2T$, odnosno $O_1Z \parallel AF$ jer će tada $EZ$ prolaziti kroz centar homotetije, odnosno dokazat ćemo zadatak. Još malo i gotovi smo, dokazat ćemo da su $O_1$ i $Z$ jednako udaljeni od $AF$. Neka su $P,Q,R$ redom nožišta okomica iz $O_1$ na $AF, ED$, te nožište okomice iz $Z$ na $AF$\\. Imamo:
\[\angle ZFR=\angle EFA=\angle EBA=\angle EDO_1\]
pa su $DQO_1$ i $ZFR$ slični s koeficijentom sličnosti $DQ/FR=DE/DF$. Konačno,
\[O_1P=OD*sin \angle O_1DP=OD*sin \angle O_2DF=OD*sin \angle O_2FD=OD*sin \angle OFA=OD*sin \angle BAF\]
\[ZR=O_1Q*DF/DE=O_1Q*sin \angle BAF/sin \angle ABE=O_1Q/sin \angle O_1DQ*sin \angle BAF=OD*sin \angle BAF\], što rješava.\\
P.S.: Čini mi se da je glavna težina zadatka gledati zadatak iz konteksta $ABC$ i dodavanje točke $T$. Također, uvijek ako imate neke uvjete na tangentne kružnice, razmislite o homotetiji kao načinu za dokazivanje konkurentnosti (još pogotovo nakon ovih početnih lemica). Zadnji se dio može činiti ružan, ali meni je on bio najlakši jer sam već shvatio ove gore lemme i stvar je bila samo chaseanja i lagane trigonometrije. Za ljubitelje projektivne geometrije, u službenom shortlist paketu ima elegantan završetak Pappusom nakon što se dobije konkurentnost prva 3 pravca, pa koga zanima može pogledati. Također, ako netko ima nekih pitanja može se javiti u komentare, postoji solidna šansa da sam napravio zatipak negdje pa ću popraviti kad budem vidio.
 presjek
presjek  i
i 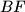 ,
,  centar
centar  , te neka je
, te neka je  presjek tangenti na
presjek tangenti na  kroz
kroz  i
i  . Također neka su
. Također neka su 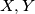 presjeci
presjeci  i
i  .
.  :
:  je na
je na 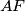 , analogno i na
, analogno i na 
 u
u  . Centar joj je
. Centar joj je  , a
, a  se šalje u polovište luka
se šalje u polovište luka  s druge strane
s druge strane  od
od  , što je upravo
, što je upravo  . Analogno je
. Analogno je  na
na  .
.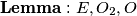 kolinearne, analogno
kolinearne, analogno 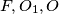 .
. :
:  je na
je na  .
. radikalno središte
radikalno središte 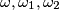
 : Trokuti
: Trokuti  i
i 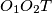 su homotetični
su homotetični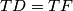 ,
, 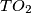 je simetrala
je simetrala 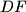 , stoga
, stoga 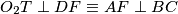 . Analogno je
. Analogno je 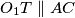 . Na kraju,
. Na kraju, 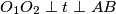 , pa su odgovarajuće stranice paralelne i to povlači našu tvrdnju.
, pa su odgovarajuće stranice paralelne i to povlači našu tvrdnju. 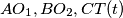 konkurentni. Cilj nam je pokazati da se ovom homotetijom i pravac
konkurentni. Cilj nam je pokazati da se ovom homotetijom i pravac  šalje u sebe. Zato neka je
šalje u sebe. Zato neka je  presjek
presjek  i
i 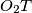 , dovoljno je pokazati da je
, dovoljno je pokazati da je 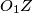 visina u
visina u 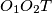 , odnosno
, odnosno 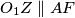 jer će tada
jer će tada 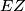 prolaziti kroz centar homotetije, odnosno dokazat ćemo zadatak. Još malo i gotovi smo, dokazat ćemo da su
prolaziti kroz centar homotetije, odnosno dokazat ćemo zadatak. Još malo i gotovi smo, dokazat ćemo da su 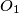 i
i  jednako udaljeni od
jednako udaljeni od 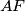 . Neka su
. Neka su 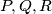 redom nožišta okomica iz
redom nožišta okomica iz 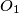 na
na 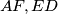 , te nožište okomice iz
, te nožište okomice iz  na
na 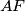
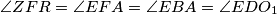 pa su
pa su 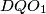 i
i 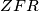 slični s koeficijentom sličnosti
slični s koeficijentom sličnosti 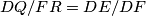 . Konačno,
. Konačno, 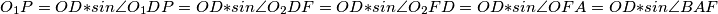
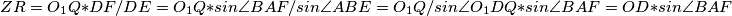 , što rješava.
, što rješava. i dodavanje točke
i dodavanje točke  . Također, uvijek ako imate neke uvjete na tangentne kružnice, razmislite o homotetiji kao načinu za dokazivanje konkurentnosti (još pogotovo nakon ovih početnih lemica). Zadnji se dio može činiti ružan, ali meni je on bio najlakši jer sam već shvatio ove gore lemme i stvar je bila samo chaseanja i lagane trigonometrije. Za ljubitelje projektivne geometrije, u službenom shortlist paketu ima elegantan završetak Pappusom nakon što se dobije konkurentnost prva 3 pravca, pa koga zanima može pogledati. Također, ako netko ima nekih pitanja može se javiti u komentare, postoji solidna šansa da sam napravio zatipak negdje pa ću popraviti kad budem vidio.
. Također, uvijek ako imate neke uvjete na tangentne kružnice, razmislite o homotetiji kao načinu za dokazivanje konkurentnosti (još pogotovo nakon ovih početnih lemica). Zadnji se dio može činiti ružan, ali meni je on bio najlakši jer sam već shvatio ove gore lemme i stvar je bila samo chaseanja i lagane trigonometrije. Za ljubitelje projektivne geometrije, u službenom shortlist paketu ima elegantan završetak Pappusom nakon što se dobije konkurentnost prva 3 pravca, pa koga zanima može pogledati. Također, ako netko ima nekih pitanja može se javiti u komentare, postoji solidna šansa da sam napravio zatipak negdje pa ću popraviti kad budem vidio.  Školjka
Školjka 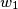 and
and 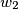 with centres
with centres 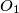 and
and 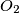 are externally tangent at point
are externally tangent at point  at points
at points  be the diameter of
be the diameter of 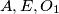 are on the same side of
are on the same side of 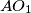 ,
, 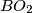 ,
, 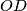 treba biti
treba biti