Neocijenjeno
1. veljače 2023. 00:14 (2 godine)
Dokažite da ne postoji polinom
s cjelobrojnim koeficijentima takav da je
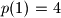
i
.
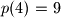
%V0
Dokažite da ne postoji polinom $p$ s cjelobrojnim koeficijentima takav da je $p(1)=4$ i $p(4)=9$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Predpodstavimo da ovaj polinom postoji jer stvarno neznam kako bi drugačije počeo.
Imamo
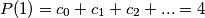
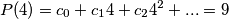
Sad malo modularna aritmetika
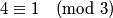Što znaći 
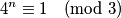Ili ti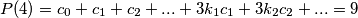 
I sada imamo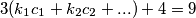 
Što je vrlo očito kontradikcija da ovaj polinom postoji.
Predpodstavimo da ovaj polinom postoji jer stvarno neznam kako bi drugačije počeo.
Imamo
$$P(1) = c_0 + c_1 + c_2 + ... = 4 $$
$$P(4) = c_0 + c_14 + c_24^2 + ... = 9 $$
Sad malo modularna aritmetika
$$4 \equiv 1 \pmod 3$$
Što znaći
$$4^n \equiv 1 \pmod 3$$
Ili ti
$$P(4) = c_0 + c_1 + c_2 + ... + 3k_1c_1 + 3k_2c_2 + ... = 9$$
I sada imamo
$$3(k_1c_1 + k_2c_2 + ... ) + 4 = 9$$
Što je vrlo očito kontradikcija da ovaj polinom postoji.
Školjka