Točno
2. veljače 2023. 22:33 (3 godine)
Nađite sva rješenja jednadžbe
![\sqrt[3]{x}+\sqrt[3]{2x-3}=\sqrt[3]{12(x-1)}.](/media/m/e/6/6/e66c679e23fcf5a20e9afab98b3819fd.png)
%V0
Nađite sva rješenja jednadžbe $$
\sqrt[3]{x}+\sqrt[3]{2x-3}=\sqrt[3]{12(x-1)}.
$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Naparavimo substituciju 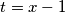
![\sqrt[3]{t + 1} + \sqrt[3]{2t - 1} = \sqrt[3]{12t}](/media/m/b/c/6/bc6bb1186748542559c983637049d64f.png) (1) ovo će bit važno za kasnije. Sad sve dignemo na treću potenciju.
(1) ovo će bit važno za kasnije. Sad sve dignemo na treću potenciju. ![(t + 1) + (2t - 1) + 3\sqrt[3]{(t + 1)(2t - 1)}(\sqrt[3]{t + 1} + \sqrt[3]{2t - 1}) = 12t](/media/m/3/1/c/31c0f842fb93717e5d491f8a741db6d9.png)
Sad uljepšajmo malo to ![\sqrt[3]{12t(t + 1)(2t - 1)} = 3t](/media/m/b/3/f/b3fa6e356c95b97e4f7b07b5281c3d1c.png) Ako se nevidi napravio sam sljedeće : prebacio sve što nije korjeni na desnu stranu , koristio (1) u zagradama , pokratio 3 sa obe strane i stavio sve pod isti korjen.
Ako se nevidi napravio sam sljedeće : prebacio sve što nije korjeni na desnu stranu , koristio (1) u zagradama , pokratio 3 sa obe strane i stavio sve pod isti korjen.
Sad sve na treću.
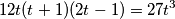
Odmah uzmimo rješenje 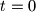 i pokratimo za ostala.
i pokratimo za ostala.
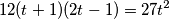
Ovo je lipo kvadratna jednađba koja se svodi na 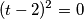 Drugo rješenje nam je
Drugo rješenje nam je 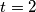
Sad sve to uvrstimo u 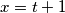
I dobijemo 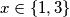
I da provjerio sam da rade ta rješenja.
Naparavimo substituciju
$t = x - 1$
$$\sqrt[3]{t + 1} + \sqrt[3]{2t - 1} = \sqrt[3]{12t}$$
(1) ovo će bit važno za kasnije.
Sad sve dignemo na treću potenciju.
$$(t + 1) + (2t - 1) + 3\sqrt[3]{(t + 1)(2t - 1)}(\sqrt[3]{t + 1} + \sqrt[3]{2t - 1}) = 12t$$
Sad uljepšajmo malo to
$$\sqrt[3]{12t(t + 1)(2t - 1)} = 3t$$
Ako se nevidi napravio sam sljedeće : prebacio sve što nije korjeni na desnu stranu , koristio (1) u zagradama , pokratio 3 sa obe strane i stavio sve pod isti korjen.
Sad sve na treću.
$$12t(t + 1)(2t - 1) = 27t^3$$
Odmah uzmimo rješenje $t = 0$ i pokratimo za ostala.
$$12(t + 1)(2t - 1) = 27t^2$$
Ovo je lipo kvadratna jednađba koja se svodi na
$$(t - 2)^2 = 0$$
Drugo rješenje nam je $t = 2$
Sad sve to uvrstimo u $x = t + 1$
I dobijemo
$$x \in \{1 , 3 \}$$
I da provjerio sam da rade ta rješenja.
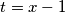
![\sqrt[3]{t + 1} + \sqrt[3]{2t - 1} = \sqrt[3]{12t}](/media/m/b/c/6/bc6bb1186748542559c983637049d64f.png) (1) ovo će bit važno za kasnije. Sad sve dignemo na treću potenciju.
(1) ovo će bit važno za kasnije. Sad sve dignemo na treću potenciju. ![(t + 1) + (2t - 1) + 3\sqrt[3]{(t + 1)(2t - 1)}(\sqrt[3]{t + 1} + \sqrt[3]{2t - 1}) = 12t](/media/m/3/1/c/31c0f842fb93717e5d491f8a741db6d9.png)
![\sqrt[3]{12t(t + 1)(2t - 1)} = 3t](/media/m/b/3/f/b3fa6e356c95b97e4f7b07b5281c3d1c.png) Ako se nevidi napravio sam sljedeće : prebacio sve što nije korjeni na desnu stranu , koristio (1) u zagradama , pokratio 3 sa obe strane i stavio sve pod isti korjen.
Ako se nevidi napravio sam sljedeće : prebacio sve što nije korjeni na desnu stranu , koristio (1) u zagradama , pokratio 3 sa obe strane i stavio sve pod isti korjen.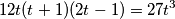
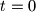 i pokratimo za ostala.
i pokratimo za ostala.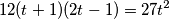
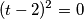 Drugo rješenje nam je
Drugo rješenje nam je 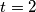
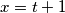
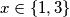
 Školjka
Školjka ![\sqrt[3]{x}+\sqrt[3]{2x-3}=\sqrt[3]{12(x-1)}.](/media/m/e/6/6/e66c679e23fcf5a20e9afab98b3819fd.png)