Neocijenjeno
2. veljače 2023. 22:59 (3 godine, 1 mjesec)
U  posuda (od kojih svaka ima barem
posuda (od kojih svaka ima barem 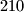 litara) nalazi se redom
litara) nalazi se redom 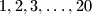 litara vode. Iz posude
litara vode. Iz posude  u posudu
u posudu  dozvoljeno je preliti točno onoliko vode koliko već ima u posudi
dozvoljeno je preliti točno onoliko vode koliko već ima u posudi  (uz pretpostavku da u posudi
(uz pretpostavku da u posudi  ima barem toliko vode koliko u
ima barem toliko vode koliko u  ). Da li je moguće nakon konačno prelijevanja dobiti:
). Da li je moguće nakon konačno prelijevanja dobiti:

 posuda s po
posuda s po  litre vode, a u preostalih
litre vode, a u preostalih  posuda po
posuda po 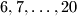 litara;
litara;
 svih
svih 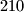 litara vode u jednoj posudi?
litara vode u jednoj posudi?
 posuda (od kojih svaka ima barem
posuda (od kojih svaka ima barem 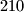 litara) nalazi se redom
litara) nalazi se redom 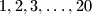 litara vode. Iz posude
litara vode. Iz posude  u posudu
u posudu  dozvoljeno je preliti točno onoliko vode koliko već ima u posudi
dozvoljeno je preliti točno onoliko vode koliko već ima u posudi  (uz pretpostavku da u posudi
(uz pretpostavku da u posudi  ima barem toliko vode koliko u
ima barem toliko vode koliko u  ). Da li je moguće nakon konačno prelijevanja dobiti:
). Da li je moguće nakon konačno prelijevanja dobiti:
 posuda s po
posuda s po  litre vode, a u preostalih
litre vode, a u preostalih  posuda po
posuda po 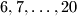 litara;
litara; svih
svih 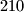 litara vode u jednoj posudi?
litara vode u jednoj posudi? Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
 Školjka
Školjka