Točno
5. veljače 2023. 12:45 (3 godine, 1 mjesec)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Žao mi je što ne mogu importati sliku iz geogebre ali dobro. Iz prvog uvjeta zaključujemo da su  -Apolonijeva kružnica u
-Apolonijeva kružnica u  i
i  -Apolonijeva u
-Apolonijeva u 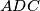 iste: neka ona ima središte
iste: neka ona ima središte  . Također neka je
. Također neka je  drugi presjek kružnica
drugi presjek kružnica 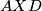 i
i 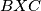 . BSO zbog položaja točaka recimo da je
. BSO zbog položaja točaka recimo da je  lijevo od
lijevo od  na
na  ,
,  unutar trokuta
unutar trokuta 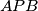
 :
:  je na
je na 
dokaz: Neka je 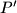 presjek
presjek  i
i 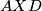 . Znamo
. Znamo 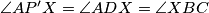 , odakle slijedi
, odakle slijedi 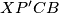 tetivan.
tetivan. : Neka je
: Neka je 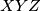 trokut i točka
trokut i točka 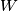 unutar njega. Tada je
unutar njega. Tada je 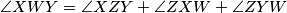
dokaz: trivijalno
Sad je ideja prebaciti konačan uvjet na  : znamo:
: znamo: 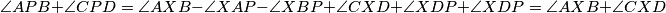 . To daje da je dovoljno pokazati da
. To daje da je dovoljno pokazati da 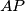 raspolavlja kut
raspolavlja kut 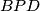 , što u kombinaciji s Apolonijevom daje da je dovoljno da je
, što u kombinaciji s Apolonijevom daje da je dovoljno da je 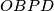 tetivan. Sad, kako je
tetivan. Sad, kako je 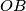 tangenta na
tangenta na  i
i 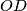 tangenta na
tangenta na 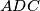 imamo
imamo 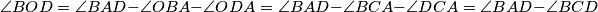
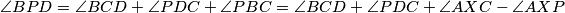
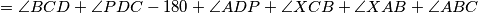
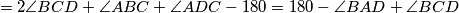 , čime smo dokazali tetivnost
, čime smo dokazali tetivnost
 Školjka
Školjka  satisfies
satisfies 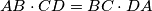 . Point
. Point  Prove that
Prove that 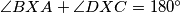 .
.