Neocijenjeno
8. siječnja 2024. 19:16 (1 godina, 3 mjeseci)
Find the least positive integer

for which there exists a set
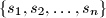
consisting of

distinct positive integers such that
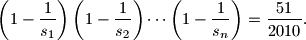
Proposed by Daniel Brown, Canada
%V0
Find the least positive integer $n$ for which there exists a set $\{s_1, s_2, \ldots , s_n\}$ consisting of $n$ distinct positive integers such that
$$\left( 1 - \frac{1}{s_1} \right) \left( 1 - \frac{1}{s_2} \right) \cdots \left( 1 - \frac{1}{s_n} \right) = \frac{51}{2010}.$$
Proposed by Daniel Brown, Canada
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Probaj $n = 1$ , $n = 2$ , $n = 3$ , $n = 4$. Rješenje je najmanji koji radi. Casework na prva tri je triv. Za $n = 4$ postoji rješenje $2$ , $3$ , $4$ , $35$.
Vrlo glup zadatak iskreno.