 be a circle and let
be a circle and let  be a line such that
be a line such that  and
and  have no common points. Further, let
have no common points. Further, let  be a diameter of the circle
be a diameter of the circle  ; assume that this diameter
; assume that this diameter  is perpendicular to the line
is perpendicular to the line  , and the point
, and the point  is nearer to the line
is nearer to the line  than the point
than the point  . Let
. Let  be an arbitrary point on the circle
be an arbitrary point on the circle  , different from the points
, different from the points  and
and  . Let
. Let  be the point of intersection of the lines
be the point of intersection of the lines  and
and  . One of the two tangents from the point
. One of the two tangents from the point  to the circle
to the circle  touches this circle
touches this circle  at a point
at a point  ; hereby, we assume that the points
; hereby, we assume that the points  and
and  lie in the same halfplane with respect to the line
lie in the same halfplane with respect to the line  . Denote by
. Denote by  the point of intersection of the lines
the point of intersection of the lines  and
and  . Let the line
. Let the line 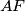 intersect the circle
intersect the circle  at a point
at a point  , different from
, different from  .
. Prove that the reflection of the point
 in the line
in the line  lies on the line
lies on the line 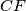 .
. Kliknite ovdje kako biste prikazali rješenje.
U rješenju, svi polovi i polare referiraju se na  . Neka je
. Neka je 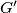 preslika
preslika  preko
preko  ,
,  presjek
presjek  i
i  .
.  je ortocentar u trokutu
je ortocentar u trokutu 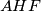 , stoga je
, stoga je 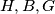 kolinearno. (
kolinearno. (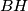 i
i 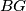 su oba okomiti na
su oba okomiti na 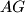 ).
). :
: 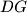 je tangenta na
je tangenta na  .
.
dokaz: Neka je  presjek
presjek  i
i 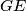 , te
, te  presjek
presjek  i
i  . Poznato je da
. Poznato je da 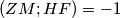 , pa projiciranjem dobivamo:
, pa projiciranjem dobivamo: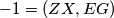 , odakle slijedi da je
, odakle slijedi da je  na polari od
na polari od  , neka je ta polara
, neka je ta polara  . Nadalje, znamo da je
. Nadalje, znamo da je  okomit na
okomit na  , pa je jedina opcija za polaru
, pa je jedina opcija za polaru  .
.
Sad, La Hire daje da je  na polari od
na polari od  , no kako je trivijalno
, no kako je trivijalno  na polari od
na polari od  imamo da je
imamo da je 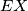 polara od
polara od  , pa je
, pa je  na toj polari i po definiciji polare slijedi tvrdnja.
na toj polari i po definiciji polare slijedi tvrdnja.
Promotrimo četverokut 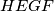 , on je tetivan zbog pravih kuteva, a kako je
, on je tetivan zbog pravih kuteva, a kako je 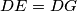 slijedi da je
slijedi da je  centar opisane mu kružnice, odnosno
centar opisane mu kružnice, odnosno  je polovište
je polovište 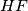 .
.
Sad slijedi ključna obzervacija:  je
je  -Humpty točka u
-Humpty točka u  Sad ide završetak zadatka: iz svojstava Humpty točke imamo:
Sad ide završetak zadatka: iz svojstava Humpty točke imamo: 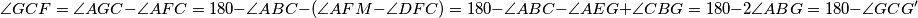 i gotovi smo
i gotovi smo
 Školjka
Školjka