Neocijenjeno
11. travnja 2023. 15:46 (2 godine, 10 mjeseci)
Neka su $a$, $b$ i $c$ realni brojevi takvi da je $a + 2b + c > 0$ i $a - 2b + c < 0$.
Dokaži da vrijedi $b^2 > ac$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Pomnožimo li nejednakosti dobijamo
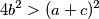 Sad dodamo li poznatu jednakost
Sad dodamo li poznatu jednakost 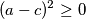 Dobijamo
Dobijamo 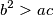
Pomnožimo li nejednakosti dobijamo
$$4b^2 > (a + c)^2$$
Sad dodamo li poznatu jednakost
$$(a - c)^2 \geq 0$$
Dobijamo
$$b^2 > ac$$