Neocijenjeno
8. rujna 2023. 15:57 (2 godine, 6 mjeseci)
Odredi sve cijele brojeve
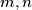
za koje vrijedi
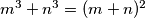
%V0
Odredi sve cijele brojeve $m, n$ za koje vrijedi $m^3+n^3=(m+n)^2$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Faktorizacija
$$(m + n)(m^2 - mn + n^2 -m - n) = 0$$
Trivijalno $m = -n$
Sad
$$m^2 -mn + n^2 - m - n$$
$$m^2 + n^2 + 1 = (m + 1)(n + 1)$$
Očito je ili
$$m + 1 > 0 , n + 1 > 0$$
Ili
$$m + 1 < 0 , n + 1 < 0$$
Znamo da je
$$m^2 + n^2 \geq 2mn$$
Za $m , n > 3$ je očito $2mn > (m + 1)(n + 1)$
I nećemo ni promatrat negativne brojeve m , n jer će onda vrijedit za sve brojeve.
Taki da ostalo nam je pogledat za $m \leq 3$
Dobijemo rješenja
$$(m , n) \in \{(0 , 1) , (1 , 0) , (1 , 2) , (2 , 1), ( 2 , 2 ) ,(k , -k)\}$$
Naravno vidia sam u rješenjima da su oni to malo pametnije s diskriminantom našli rjesenja.