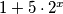
Odredi sve cijele brojeve takve da je kvadrat racionalnog broja.
%V0
Odredi sve cijele brojeve $x$ takve da je $1 + 5 \cdot 2^x$ kvadrat racionalnog broja.
Upozorenje: Ovaj zadatak još niste riješili! Kliknite ovdje kako biste prikazali rješenje.
Prvo provjerimo za Tu dobijemo rješenje , Sad za Zato što su ti razlomci u skračenom obliku zaključujemo da mora biti Tjst
Prvo provjerimo za $x\geq 0$
$$5\cdot 2^x = (n - 1)(n +1)$$
Tu dobijemo rješenje $n = 9$ , $x = 4$
Sad za $x < 0$
$$\frac{5}{2^y} = \frac{p^2 - q^2}{q^2}$$
Zato što su ti razlomci u skračenom obliku zaključujemo da mora biti
$$5 = p^2 - q^2$$
Tjst $x = -2$
Školjka 
takve da je 
kvadrat racionalnog broja. 
Tu dobijemo rješenje 
, 
Sad za 
Zato što su ti razlomci u skračenom obliku zaključujemo da mora biti 
Tjst 