Neocijenjeno
8. rujna 2023. 16:44 (1 godina, 5 mjeseci)
Dano je
složenih prirodnih brojeva manjih od
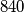
. Dokaži da među njima postoje barem dva broja koja nisu relativno prosta.
%V0
Dano je $10$ složenih prirodnih brojeva manjih od $840$. Dokaži da među njima postoje barem dva broja koja nisu relativno prosta.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Očito je da svaki složen broj manji od 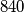mora imat jedan od faktora : 
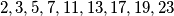To je ono najmanji faktor broja n je manji ili jednak od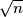 
Sad imamo 9 tih faktora i 10 brojeva. Pa sad moš stavljat golube u kaveze.
Očito je da svaki složen broj manji od $840$ mora imat jedan od faktora :
$$2 , 3 , 5 , 7 , 11 , 13 , 17 , 19 , 23$$
To je ono najmanji faktor broja n je manji ili jednak od $\sqrt{n}$
Sad imamo 9 tih faktora i 10 brojeva. Pa sad moš stavljat golube u kaveze.
Školjka