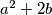
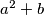
Neka su i cijeli brojevi takvi da je kvadrat cijelog broja. Dokaži da se broj može prikazati kao zbroj kvadrata dvaju cijelih brojeva.
%V0
Neka su $a$ i $b$ cijeli brojevi takvi da je $a^{2} + 2b$ kvadrat cijelog broja. Dokaži da se broj $a^{2} + b$ može prikazati kao zbroj kvadrata dvaju cijelih brojeva.
Upozorenje: Ovaj zadatak još niste riješili! Kliknite ovdje kako biste prikazali rješenje.
i su iste parnosti. To je valjda očito.
$$b = \frac{n^2 - a^2}{2}$$
$$a^2 + b = \frac{a^2 + n^2}{2} = \frac{(a + n)^2 + (a - n)^2}{4} = \left(\frac{a + n}{2}\right)^2 + \left(\frac{a - n}{2}\right)^2$$
$a$ i $n$ su iste parnosti. To je valjda očito.
Školjka 
i 
cijeli brojevi takvi da je 
kvadrat cijelog broja. Dokaži da se broj 
može prikazati kao zbroj kvadrata dvaju cijelih brojeva. 
su iste parnosti. To je valjda očito.