Neocijenjeno
18. rujna 2023. 18:40 (7 mjeseci, 2 tjedna)
Skakavac se na početku nalazi u ishodištu brojevnog pravca, na broju  , a zatim skače uvijek u istom smjeru. Za prirodni broj
, a zatim skače uvijek u istom smjeru. Za prirodni broj  , skakavac u prvom skoku dolazi na broj
, skakavac u prvom skoku dolazi na broj  , a svaki sljedeći skok je točno
, a svaki sljedeći skok je točno  puta dulji od prethodnog. Na mjestu svakog višekratnika broja
puta dulji od prethodnog. Na mjestu svakog višekratnika broja 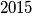 nalazi se rupa.
nalazi se rupa.
Odredi sve prirodne brojeve takve da skakav može skočiti
takve da skakav može skočiti 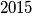 puta, a da pritom ne uskoči u rupu.
puta, a da pritom ne uskoči u rupu.
 , a zatim skače uvijek u istom smjeru. Za prirodni broj
, a zatim skače uvijek u istom smjeru. Za prirodni broj  , skakavac u prvom skoku dolazi na broj
, skakavac u prvom skoku dolazi na broj  , a svaki sljedeći skok je točno
, a svaki sljedeći skok je točno  puta dulji od prethodnog. Na mjestu svakog višekratnika broja
puta dulji od prethodnog. Na mjestu svakog višekratnika broja 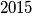 nalazi se rupa.
nalazi se rupa.Odredi sve prirodne brojeve
 takve da skakav može skočiti
takve da skakav može skočiti 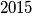 puta, a da pritom ne uskoči u rupu.
puta, a da pritom ne uskoči u rupu. Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Ajmo dokazat da je 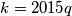 Pretpodstavi da je
Pretpodstavi da je 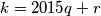 takav da nikoji od
takav da nikoji od 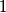
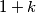
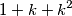

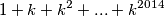 Nije djeljiv s
Nije djeljiv s 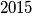 onda imamo
onda imamo 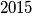 brojeva i
brojeva i 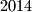 mogućih ostataka. Tako da dobijemo da :
mogućih ostataka. Tako da dobijemo da : 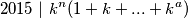
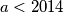 I odavde imamo da
I odavde imamo da 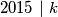 kontradikcija s činjenicom da je
kontradikcija s činjenicom da je 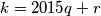 Što znaći da je
Što znaći da je 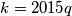 i to zaista radi jer će ostatak uvjek biti
i to zaista radi jer će ostatak uvjek biti  tako da nikad neće upast u rupu.
tako da nikad neće upast u rupu.
Ok izgleda da sam za jednu oktavu falia. Zato što samo to što 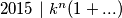 ne znaći da
ne znaći da 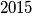 djeli
djeli  Trebao sam promatrat slučaje gdje je
Trebao sam promatrat slučaje gdje je 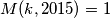 i doć do kontradikcije.
i doć do kontradikcije.
 Školjka
Školjka