Neocijenjeno
23. travnja 2023. 20:01 (1 godina, 11 mjeseci)
Nađite sve
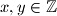
za koje vrijedi
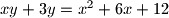
.
%V0
Nađite sve $x,y\in\mathbb{Z}$ za koje vrijedi $xy+3y=x^2+6x+12$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
xy + 3y = x^2 + 6x + 12 y(x + 3) = (x + 3)^2 + 3 y= ((x+3)^2 + 3) / (x + 3) y = x + 3+ 3 / (x+3) Kako su y, x i 3 cijeli brojevi, 3 / (x+3) mora isto biti cijeli broj što znači da je x + 3 djelitelj od 3. Dakle: x= -2 y= 4, x= 0 y= 4, x= -6 y= -4, x= -4 y= -4.
xy + 3y = x^2 + 6x + 12
y(x + 3) = (x + 3)^2 + 3
y= ((x+3)^2 + 3) / (x + 3)
y = x + 3+ 3 / (x+3)
Kako su y, x i 3 cijeli brojevi, 3 / (x+3) mora isto biti cijeli broj što znači da je x + 3 djelitelj od 3.
Dakle:
x= -2 y= 4,
x= 0 y= 4,
x= -6 y= -4,
x= -4 y= -4.