Neocijenjeno
16. svibnja 2023. 18:37 (2 godine, 9 mjeseci)
Na ploči su napisani brojevi
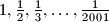
. Učenik odabire dva broja s ploče, recimo

i

, te izračuna broj
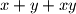
, rezultat zapiše na ploču, a

i

obriše. Odredite broj koji će ostati na ploči nakon što ovaj postupak obavi
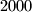
puta.
%V0
Na ploči su napisani brojevi $1, \frac 12, \frac 13, \ldots, \frac{1}{2001}$. Učenik odabire dva broja s ploče, recimo $x$ i $y$, te izračuna broj $x + y + xy$, rezultat zapiše na ploču, a $x$ i $y$ obriše. Odredite broj koji će ostati na ploči nakon što ovaj postupak obavi $2000$ puta.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Indukcijom ćemo dokazat da je odg 1
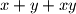 je komutativno što znaći da nas nije briga za redosljed.
je komutativno što znaći da nas nije briga za redosljed.
Prebacimo zad tako da umisto da radimo x + y + xy , mi radimo 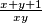 i brojevi :
i brojevi : 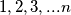 Nek nam baza bude
Nek nam baza bude 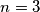 i onda ćemo dokazat za
i onda ćemo dokazat za 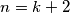
Za 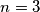 to vrijedi. Sad pretpodstavimo da to vrijedi za
to vrijedi. Sad pretpodstavimo da to vrijedi za 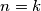
Dokaz za 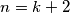 Imamo brojeve
Imamo brojeve
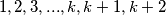 Napravimo one korake da dobijemo :
Napravimo one korake da dobijemo : 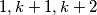 Ova tri broja se pretvore u 1 nakon one funkcije ili kako god se zove.
Ova tri broja se pretvore u 1 nakon one funkcije ili kako god se zove.
Znaći to čudo je 1 za svaki neparan n veći od 1
Indukcijom ćemo dokazat da je odg 1
$x + y + xy$ je komutativno što znaći da nas nije briga za redosljed.
Prebacimo zad tako da umisto da radimo x + y + xy , mi radimo $\frac{x + y + 1}{xy}$ i brojevi : $1 , 2 , 3 , ...n$
Nek nam baza bude $n = 3$ i onda ćemo dokazat za $n = k + 2$
Za $n = 3$ to vrijedi. Sad pretpodstavimo da to vrijedi za $n = k$
Dokaz za $n = k + 2$
Imamo brojeve
$$1 , 2 , 3 ,... , k , k + 1 , k + 2$$
Napravimo one korake da dobijemo :
$$1 , k + 1 , k + 2$$
Ova tri broja se pretvore u 1 nakon one funkcije ili kako god se zove.
Znaći to čudo je 1 za svaki neparan n veći od 1
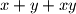 je komutativno što znaći da nas nije briga za redosljed.
je komutativno što znaći da nas nije briga za redosljed.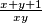 i brojevi :
i brojevi : 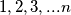 Nek nam baza bude
Nek nam baza bude 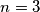 i onda ćemo dokazat za
i onda ćemo dokazat za 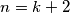
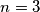 to vrijedi. Sad pretpodstavimo da to vrijedi za
to vrijedi. Sad pretpodstavimo da to vrijedi za 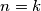
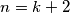 Imamo brojeve
Imamo brojeve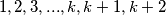 Napravimo one korake da dobijemo :
Napravimo one korake da dobijemo : 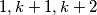 Ova tri broja se pretvore u 1 nakon one funkcije ili kako god se zove.
Ova tri broja se pretvore u 1 nakon one funkcije ili kako god se zove. Školjka
Školjka 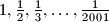 . Učenik odabire dva broja s ploče, recimo
. Učenik odabire dva broja s ploče, recimo  i
i  , te izračuna broj
, te izračuna broj 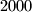 puta.
puta.