Točno
7. srpnja 2023. 16:05 (2 godine, 8 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Vidimo da f(x) = 0 za svaki x zadovoljava jednadžbu
Nadalje neka je c realan broj takav da f(c) nije jednak nuli.
Neka f(a) = f(b)
Uvrštavanjem (c, a) i (c, b) u početnu jednadžbu dobivamo:
f(c f(a)) + f(f(c) + f(a)) = a f(c) + f(c + f(a)) i
f(c f(b)) + f(f(c) + f(b)) = b f(c) + f(c + f(b)), oduzimanjem jednadžbi koristeći f(a) = f(b) dobivamo
0 = f(c) (a - b) i kako f(c) nije nula
0 = a - b odnosno a = b što je injektivnost
Uvrštavanjem (0, 1) u početnu jednadžbu dobije se:
f(0) + f(f(0) + f(1)) = f(0) + f(f(1))
f(f(0) + f(1)) = f(f(1)) zbog injektivnosti je
f(0) + f(1) = f(1) odnosno f(0) = 0
Sada uvrštavanjem y = 0 u početnu jednadžbu dobije se
f(f(x)) = f(x) i po injektivnosti
f(x) = x što radi kao rješenje
 Školjka
Školjka 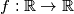 , such that
, such that 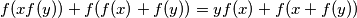 holds for all
holds for all  ,
, 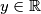 , where
, where 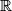 denotes the set of real numbers.
denotes the set of real numbers.