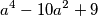
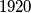
Dokažite da je izraz djeljiv s za svaki prosti broj .
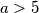
%V0
Dokažite da je izraz $$a^4-10a^2+9$$ djeljiv s $1920$ za svaki prosti broj $a > 5$.
Upozorenje: Ovaj zadatak još niste riješili! Kliknite ovdje kako biste prikazali rješenje.
Trivijalno je da je taj izraz djeljiv s .
Razlikujemo dva slućaja Uvrštavajući u faktoriziran oblik : Vidimo da je broj djeljiv i sa
$$1920 = 3\cdot 5 \cdot 2^7$$
Trivijalno je da je taj izraz djeljiv s $15$.
Razlikujemo dva slućaja $p = 4k + 1 , 4k + 3$
Uvrštavajući u faktoriziran oblik :
$$(a - 3)(a + 3)(a - 1)(a + 1)$$
Vidimo da je broj djeljiv i sa $128$
Školjka 
djeljiv s 
za svaki prosti broj 
. 
Trivijalno je da je taj izraz djeljiv s 
.
Uvrštavajući u faktoriziran oblik : 
Vidimo da je broj djeljiv i sa 