Točno
7. rujna 2023. 14:50 (8 mjeseci)
Za koje cijele brojeve
je
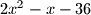
kvadrat prostog broja?
%V0
Za koje cijele brojeve $x$ je $2x^2 - x - 36$ kvadrat prostog broja?
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
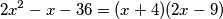Treba samo pogledat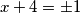i
i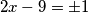 
Provjerom dobijemo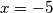 
i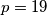 
Zapravo se pitalo da to bude kvadrat prostog broja. Al necu nista ispravljat ako sam vec vidia rjesenja. Ugl glavna ideja je tu (faktorizacija)
$$2x^2 - x - 36 = (x + 4)(2x - 9)$$
Treba samo pogledati
$$x + 4 = \pm 1$$
i
$$2x - 9 = \pm 1$$
Provjerom dobijemo $x = -5$ i $p = 19$
Zapravo se pitalo da to bude kvadrat prostog broja. Al necu nista ispravljat ako sam vec vidia rjesenja. Ugl glavna ideja je tu (faktorizacija)
| 29. rujna 2023. 10:36 | prv123 | Točno |
Školjka