Neocijenjeno
7. rujna 2023. 15:39 (1 godina, 5 mjeseci)
Koliko ima djelitelja broja
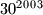
koji nisu djelitelji broja
?
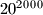
%V0
Koliko ima djelitelja broja $30^{2003}$ koji nisu djelitelji broja $20^{2000}$?
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
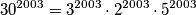
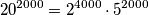
Djelitelji prvog broja koji djele i drugi broj oblika su :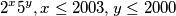 
Tako da rješenje je
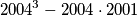
$$30^{2003} = 3^{2003} \cdot 2^{2003} \cdot 5^{2003} $$
$$20^{2000} = 2^{4000} \cdot 5^{2000}$$
Djelitelji prvog broja koji djele i drugi broj oblika su :
$$2^x 5^y , x \leq 2003 , y \leq 2000$$
Tako da rješenje je
$$2004^3 - 2004 \cdot 2001$$
Školjka