Neocijenjeno
7. rujna 2023. 18:40 (2 godine, 5 mjeseci)
Odredite najveći prirodni broj

takav da
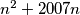
bude kvadrat nekog prirodnog broja.
%V0
Odredite najveći prirodni broj $n$ takav da $n^2 + 2007n$ bude kvadrat nekog prirodnog broja.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Amo reć da je da je $gcd(n , 2007) = k$ , $n = xk$
Onda je
$$k^2x(x + \frac{2007}{k}) = m^2$$
Tjst $x = y^2$
i
$$y^2 + \frac{2007}{k} = s^2$$
$$(s - y)(s + y) = \frac{2007}{k}$$
$$s - y = a$$
$$s + y = b$$
$$y = \frac{b- a}{2}$$
Očito da bi y bio maks mora vrijedit $b = \frac{2007}{k}$ i $a = 1$
$$y = \frac{2007 - k}{2k}$$
$$x = \frac{(2007 - k)^2}{4k^2}$$
$$n = \frac{2007^2 - 2\cdot 2007k + k^2}{4k}$$
Derivacija ovog čuda je negativna pa je k = 1.
$$n = 1003^2$$
Ok ovo je ocajno rjesenje. Al tocno je