Neocijenjeno
7. rujna 2023. 19:46 (1 godina, 5 mjeseci)
Koliko ima peteroznamenkastih brojeva oblika
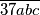
takvih da je svaki od brojeva
,
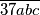
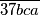
i
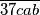
djeljiv s
?
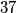
%V0
Koliko ima peteroznamenkastih brojeva oblika $\overline{37abc}$ takvih da je svaki od brojeva $\overline{37abc}$, $\overline{37bca}$ i $\overline{37cab}$ djeljiv s $37$?
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Ako je
$$37 | \overline{abc}$$
I znamo da
$$37 | \overline{abc0} - \overline{bca}$$
Dobijamo da za svaki broj $$\overline{37abc}$$ koji je djeljiv s $37$ sva tri broja su djeljiva s $37$
Prvi takav broj je $37000 = 37\cdot 1000$ a zadnji je $37999 = 37\cdot 1027$ tako da tih brojeva ima
Takvih brojeva ima $28$
Školjka 
I znamo da 
Dobijamo da za svaki broj 
koji je djeljiv s 
a zadnji je 
tako da tih brojeva ima