Neocijenjeno
26. listopada 2023. 20:41 (1 godina)
U šesterokutu
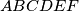
vrijedi
Ako su duljine stranica tog šesterokuta prirodni brojevi, dokaži da ne mogu svi biti neparni.
%V0
U šesterokutu $ABCDEF$ vrijedi $$ AB \perp BC \text{,} \qquad AC \perp CD \text{,} \qquad AD \perp DE \text{,} \qquad AE \perp EF \text{.} $$ Ako su duljine stranica tog šesterokuta prirodni brojevi, dokaži da ne mogu svi biti neparni.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Oznaćimo $AB$ sa $a_1$ , $BC$ sa $a_2$ i ostale stranice analogno.
Primjetimo da vrijedi :
\[a_1^2 + a_2^2 + a_3^2 + a_4^2 + a_5^2 = a_6^2\]
Pretpodstavimo da su svi $a_i$ neparni.
Tvrdnja zadatka nas motivira da gledamo $\pmod 2$ , $\pmod 4$ , $\pmod 8$
Probavanjem vidimo da $\pmod 8$ daje kontradikciju.
Školjka 
sa 
, 
sa 
i ostale stranice analogno.
neparni. Tvrdnja zadatka nas motivira da gledamo 
, 
, 