Neocijenjeno
7. rujna 2023. 22:03 (2 godine, 6 mjeseci)
U decimalnom zapisu broj
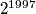
ima

znamenaka, a u zapisu broja
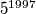
ima

znamenaka. Kolika je suma

?
%V0
U decimalnom zapisu broj $2^{1997}$ ima $m$ znamenaka, a u zapisu broja $5^{1997}$ ima $n$ znamenaka. Kolika je suma $m+n$?
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Ok znaci
$$m = \left\lfloor \log_{10} 2^{1997} \right\rfloor + 1$$
$$n = \left\lfloor \log_{10} 5^{1997} \right\rfloor + 1$$
Zato što je $$log_{10} 2^{1997} + log_{10} 5^{1997}$$ prirodan broj tjst $1997$
Zaključujemo da je broj znamenki $1998$
Evo neki dokaz
$$\lfloor a \rfloor + \lfloor b \rfloor = \lfloor a + b \rfloor - 1$$
Kada a i b nisu cijeli brojevi ali a + b je.
Stavimo
$a = x + p , x \in \mathbb{N}$
$b = y + q , y \in \mathbb{N}$
Onda mora biti $p + q = 1$
I zato ispada
$$x + y = (x + y + 1) - 1$$