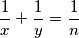
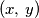
Odredite sve pozitivne cijele brojeve za koje jednadžba ima točno pet rješenja u skupu pozitivnih cijelih brojeva.
%V0
Odredite sve pozitivne cijele brojeve $n$ za koje jednadžba $$\frac1x + \frac1y = \frac1n$$ ima točno pet rješenja $\left(x,\,y\right)$ u skupu pozitivnih cijelih brojeva.
Upozorenje: Ovaj zadatak još niste riješili! Kliknite ovdje kako biste prikazali rješenje.
Klasična faktorizacija
Gledajmo to ovako Kad bi oba faktora bila pozitivna dobili bi broj manji od stoga mora vrijediti
Sad gledajmo da tjst oni mogu postić sve vrijednosti.
Zato što ima točno 5 rješenje to znaći da ima 5 faktora tjst
Klasična faktorizacija
$$(x - n)(y - n) = n^2$$
Gledajmo to ovako
$$(n - x)(n - y) = n^2$$
Kad bi oba faktora bila pozitivna dobili bi broj manji od $n^2$ stoga mora vrijediti $x > n , y > n$
Sad gledajmo da $x - n , y - n = \mathbb{N}$ tjst oni mogu postić sve vrijednosti.
Zato što ima točno 5 rješenje to znaći da $n^2$ ima 5 faktora tjst $n = p^2$
Školjka 
za koje jednadžba 
ima točno pet rješenja 
u skupu pozitivnih cijelih brojeva. 
Gledajmo to ovako 
Kad bi oba faktora bila pozitivna dobili bi broj manji od 
stoga mora vrijediti 
tjst oni mogu postić sve vrijednosti.