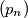
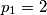
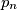
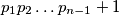
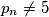
Brojevi za definirani su na sljedeći način: i za , je najveći prosti djelitelj od . Dokažite da je za svaki .
%V0
Brojevi $(p_n)$ za $n \in \mathbb{N}$ definirani su na sljedeći način:
$p_1 = 2$ i za $n \geq 2$, $p_n$ je najveći prosti djelitelj od $p_1p_2 \dots p_{n-1} + 1$. Dokažite da je $p_n \not= 5$ za svaki $n \in \mathbb{N}$.
Upozorenje: Ovaj zadatak još niste riješili! Kliknite ovdje kako biste prikazali rješenje.
Uočimo da 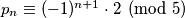Ovo možemo dokazat indukcijom.
Uočimo da $p_n \equiv (-1)^{n + 1}\cdot 2 \pmod 5$
Ovo možemo dokazat indukcijom.
Školjka 
za 
definirani su na sljedeći način:
i za 
, 
je najveći prosti djelitelj od 
. Dokažite da je 
za svaki 
Ovo možemo dokazat indukcijom.